设M(x,y,z)为空间内一点,并设点M在xOy面上的投影P的极坐标为(ρ,θ),则这样的3个数ρ,θ,z就称为点M的柱面坐标(见图11-5),这里规定ρ,θ,z的变化范围为
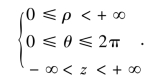
点M的直角坐标(x,y,z)与柱面坐标(ρ,θ,z)的关系为

柱面坐标系中的三簇坐标面分别为:
ρ=常数,即以z轴为轴的圆柱面;
θ=常数,即过z轴的半平面;
z=常数,即与xOy面平行的平面.
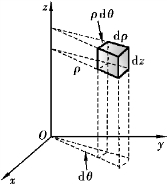
现在来考察三重积分在柱面坐标系下的形式.为此,用柱面坐标系中的三簇坐标面把空间区域Ω划分为许多小闭区域,除了含Ω的边界点的一些不规则小闭区域外,这种小闭区域都是柱体.考虑由ρ,θ,z各取得微小增量dρ,dθ,dz所围成柱体的体积,如图11-6所示.
在不计高阶无穷小时,这个柱体的体积可近似看成边长为ρdθ,dρ,dz的长方体的体积,故得到柱面坐标系中的体积元素
![]()
简单来说,dxdy=ρdρdθ,dxdydz=dxdy·dz=ρdρdθdz.再利用关系式(11-5),就得到柱面坐标系中的三重积分
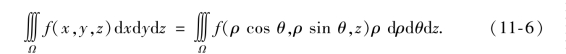

图11-5
 (https://www.xing528.com)
(https://www.xing528.com)
图11-6
为了把式(11-6)右端的三重积分化为累次积分,假定平行于z轴的直线与区域Ω的边界最多只有两个交点.设Ω在xOy面上的投影为Dxy,区域Dxy用ρ,θ表示.区域Ω关于xOy面的投影柱面将Ω的边界曲面分为上下两部分,设下曲面方程为z=z1(ρ,θ),上曲面方程为z=z2(ρ,θ),z1(ρ,θ)≤z≤z2(ρ,θ),(ρ,θ)∈Dxy,于是

注 采用柱面坐标按上述公式计算三重积分,实际上是对z采用直角坐标进行积分,而对另两个变量采用平面极坐标变换进行积分.
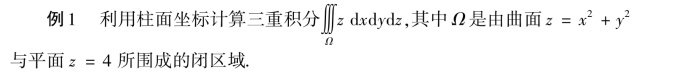
解 闭区域Ω可表示为
![]()
于是

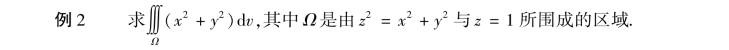
解 闭区域Ω可表示为
![]()
于是
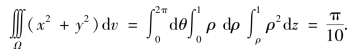
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




