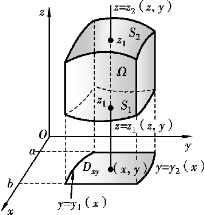
图11-1
假设平行于z轴且穿过闭区域Ω内部的直线与闭区域Ω的边界曲面S相交不多于两点.把闭区域Ω投影到xOy面上,得一平面闭区域Dxy(见图11-1),以Dxy的边界为准线作母线平行于z轴的柱面.此柱面与曲面S的交线从S中分出上下两部分,它们的方程分别为
![]()
其中,z1(x,y)与z2(x,y)都是Dxy上的连续函数,且z1(x,y)≤z2(x,y).过Dxy内任意一点(x,y)作平行于z轴的直线,这一直线通过曲面S1穿入Ω内,然后通过曲面S2穿出Ω外,穿入点和穿出点的竖坐标分别为z1(x,y),z2(x,y).于是,积分区域Ω可表示为
![]()
首先将x,y看成定值,而将f(x,y,z)只看成z的函数,在区间[z1(x,y),z2(x,y)]上对z积分.积分的结果是x,y的函数,记为F(x,y),即
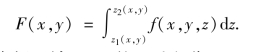
然后计算F(x,y)在闭区域Dxy上的二重积分
![]()
假如闭区域
![]()
把这个二重积分化为二次积分,则得到三重积分的计算公式
![]()
式(11-3)把三重积分化为先对z再对y,最后对x的三次积分.
如果平行于x轴或y轴且穿过闭区域Ω内部的直线与Ω的边界曲面S相交不多于两点,也可把闭区域Ω投影到yOz面上或zOx面上,这样便可把三重积分化为其他顺序的三次积分.如果平行于坐标轴且穿过闭区域Ω内部的直线与边界曲面S的交点多于两个,也可像处理二重积分那样,把Ω分成若干部分,使Ω上的三重积分化为各部分闭区域上的三重积分的和.
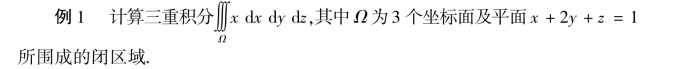
解 作出闭区域Ω,如图11-2所示.(https://www.xing528.com)
将Ω投影到xOy面上,得到的投影区域Dxy为三角形闭区域OAB.直线OA,OB及AB的方程依次为y=0,x=0及x+2y=1,故
![]()
在Dxy内任取一点(x,y),过此点作平行于z轴的直线,该直线通过平面z=0穿过Ω内,然后通过平面z=1-x-2y穿出Ω外,即有0≤z≤1-x-2y.于是
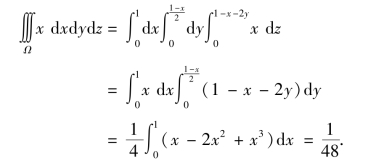
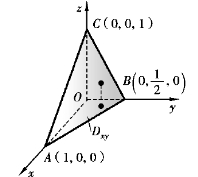
图11-2

解 曲面z=x2+2y2为开口向上的椭圆抛物面,而z=2-x2为母线平行于y轴的开口向下的抛物柱面,解方程组
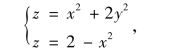
即可得到这两个曲面的交线为x2+y2=1.由此可知,这两个曲面所围成的空间立体Ω的投影区域为Dxy:x2+y2≤1.由这两个曲面的图形特征可知,在投影区域Dxy上,z=2-x2为上曲面,z=x2+2y2为下曲面.于是,积分区域Ω可表示为
![]()
所以
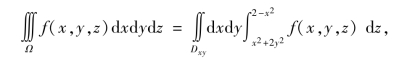
而投影区域Dxy的积分限为
![]()
于是
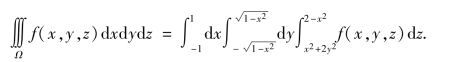
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




