微积分（下册）：正弦和余弦级数

一般来说，一个函数的傅里叶级数会同时含有正弦项和余弦项.但是，也会存在一些函数的傅里叶展开式只含有其中的一种，其原因与所给函数f（x）的奇偶性有关.对周期为2π的周期函数f（x），它的傅里叶系数的计算公式为

由于奇函数在对称区间上的积分为零，偶函数在对称区间上的积分等于半区间上积分的2倍，因此，当f（x）为奇函数时，f（x）cos nx是奇函数，f（x）sin nx是偶函数，故

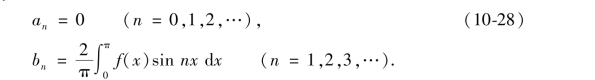
可知，奇函数的傅里叶级数是只含有正弦项的正弦级数

当f（x）为偶函数时，f（x）cos nx是偶函数，f（x）sin nx是奇函数，故

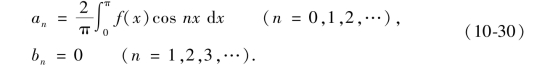
可知，偶函数的傅里叶级数是只含有常数项和余弦项的余弦级数

例4　设f（x）是周期为2π的周期函数，它在[-π，π）上的表达式为f（x）=x.将f（x）展开成傅里叶级数，并作出级数的和函数的图形.

解　首先，所给函数满足收敛定理的条件，它在点

处不连续.因此，f（x）的傅里叶级数在点x=（2k+1）π处收敛于

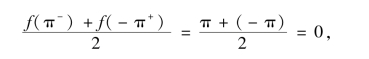
在连续点x（x≠（2k+1）π）处收敛于f（x）.

其次，若不计x=（2k+1）π（k=0，±1，±2，…），则f（x）是周期为2π的奇函数.显然，此时按照式（10-28）有an=0（n=0，1，2，…），而

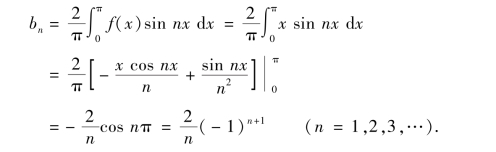
将求得的bn代入正弦级数（10-29），得f（x）的傅里叶级数展开式为

级数的和函数的图形如图10-5所示.

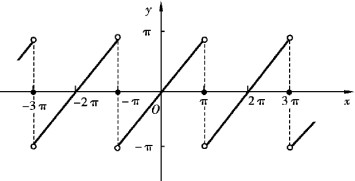
图10-5

解　所给函数满足收敛定理的条件，它在整个数轴上连续.因此，f（x）的傅里叶级数处处收敛于f（x）.

因为f（x）是偶函数，所以按式（10-30），有bn=0（n=1，2，3，…），而

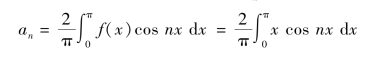
将系数代入余弦级数（10-31），得f（x）的傅里叶级数展开式为

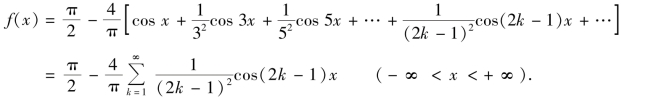
在实际应用中，有时还需要把定义在区间[0，π]上的函数f（x）展开成正弦级数或者余弦级数.

根据前面讨论的结果，这类展开问题解决方法为：设函数f（x）定义在区间[0，π]上并且满足收敛定理的条件，在开区间（-π，0）内补充f（x）的定义，可得定义在（-π，π]上的函数F（x），使它在（-π，π）上成为奇函数（偶函数）.按这种方式拓广函数定义域的过程，称为奇延拓（偶延拓）.然后将延拓后的函数展开成傅里叶级数，这个级数必定是正弦级数（余弦级数）.再限制x在（0，π]上，此时F（x）≡f（x），这样便得到f（x）的正弦级数（余弦级数）展开式.

例如，将函数

(www.xing528.com)

作奇延拓，再作周期延拓，便成例4中的函数，根据例4的结果，有

将φ（x）作偶延拓，再作周期延拓，便成例5中的函数，根据其结果，有

注　利用函数的傅里叶级数展开式，有时可得到一些特殊级数的和.例如，根据例5的结果，有

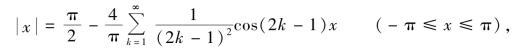
在上式中令x=0，得

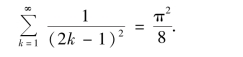
设

因为

所以

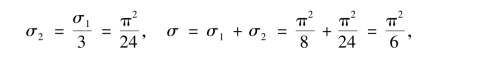
又

在上述讨论的例子中，周期函数都是以2π为周期，但实际生活中所遇到的周期函数，它的周期不一定是2π.因此，就需要作适当的变量代换.

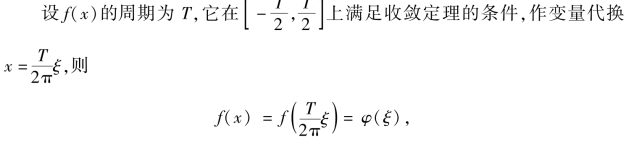
那么，φ（ξ）是[-π，π]上的以2π为周期的周期函数，于是有

此处，故

例6　将以下函数展开为正弦级数

解　先对f（x）作奇延拓，延拓后得到

则

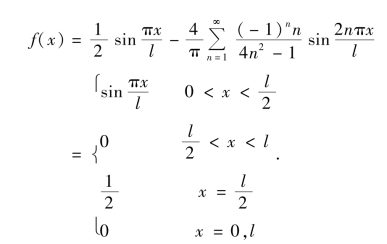
其傅里叶级数的图形如图10-6所示.

图10-6