微积分（下册）：函数傅里叶级数展开效果

设f（x）是周期为2π的周期函数，且能展开成三角级数

我们自然要考虑系数a0，a1，b1，…与函数f（x）之间存在着怎样的关系.换句话说，如何利用f（x）把a0，a1，b1，…求出来.为此，假设式（10-25）右端可以逐项积分.

先求a0.对式（10-25）从-π到π积分，由于假设式（10-25）右端可逐项积分，故有

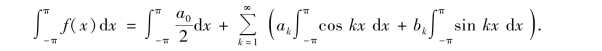
根据三角函数系的正交性可知，等式右端除第一项之外，其余都为零，故

于是有

　再求an.对式（10-25）两端乘以cos nx，再从-π到π积分得

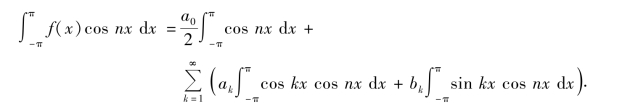
根据三角函数系的正交性，上式的右端除k=n的一项之外，其余项全为零，故

于是有

类似地，用sin nx乘以式（10-25）的两端，再从-π到π积分得

因此，式（10-25）的各系数表达式可合并成

如果式（10-26）中的积分都存在，此时由式（10-26）得出的系数a0，a1，b1，…称为函数f（x）的傅里叶系数，将这些系数代入式（10-25）的右端，得到的三角级数

称为函数f（x）的傅里叶级数.

下面介绍一个收敛定理，它是傅里叶级数收敛的重要结论.

定理1（收敛定理，狄利克雷充分条件）　设f（x）是周期为2π的周期函数，如果满足：

（1）在一个周期内连续或者只有有限个第一类间断点；

（2）在一个周期内至多只有有限个极值点，

那么，f（x）的傅里叶级数收敛，并且：

当x是f（x）的连续点时，级数收敛于f（x）；

上述定理说明，只要函数在[-π，π]上有有限个第一类间断点，并且不作无限次的振动，那么函数的傅里叶级数在连续点处就收敛于该点的函数值，在间断点处就收敛于该点处函数的左右极限的算术平均数，记

在C上就成立f（x）的傅里叶级数展开式

例1　设f（x）是周期为2π的周期函数，它在[-π，π）上的表达式为

将f（x）展开成傅里叶级数，并作出级数的和函数的图形.

解　可知所给函数f（x）满足收敛定理中的条件，在x=kπ（k=0，±1，±2，…）处不连续，在其他点处连续.由收敛定理可知，函数f（x）的傅里叶级数收敛，并且当x=kπ时，级数收敛于(www.xing528.com)

当x≠kπ时，级数收敛于f（x）.

傅里叶系数的计算为

　将所求系数代入式（10-27）得到f（x）的傅里叶级数展开式

级数的和函数图形如图10.2所示.

图10-2

例2　设f（x）是以2π为周期的周期函数，它在[-π，π]上的表达式为

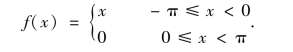
将f（x）展开成傅里叶级数，并作出级数的和函数的图形.

解　所给函数满足收敛定理的条件，它在点x=（2k+1）π（k=0，±1，±2，…）处间断.因此，当x≠（2k+1）π时，函数f（x）的傅里叶级数收敛于f（x）；当x=（2k+1）π时，函数f（x）的傅里叶级数收敛于

函数f（x）的傅里叶系数计算为

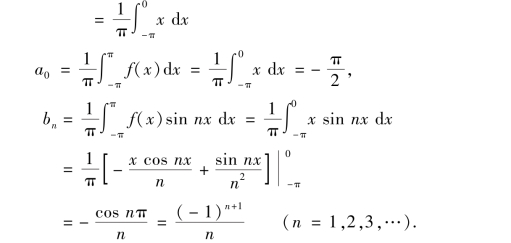
将所求得的系数代入式（10-27），得到f（x）的傅里叶级数展开式

级数的和函数的图形如图10-3所示.

图10-3

应该注意，如果函数f（x）只在[-π，π]上有定义，并且满足收敛定理的条件，那么函数f（x）也可展开成傅里叶级数.事实上，可在[-π，π）或（-π，π]外补充函数f（x）的定义，使它拓广成周期为2π的周期函数F（x）.按这种方式拓广函数的定义域的过程，称为周期延拓.再将F（x）展开成傅里叶级数.最后限制x在（-π，π）内，此时F（x）≡f（x），这样便得到f（x）的傅里叶级数展开式.根据收敛定理，这级数在区间端点x=±π处收敛于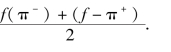

例3　将函数

展开成傅里叶级数.

解　题中所给函数在[-π，π]上满足收敛定理的条件，若将其拓展为周期函数，则此周期函数在每一点t处都是连续的（见图10-4），因此，拓展的周期函数的傅里叶级数在[-π，π]内收敛于f（t）.

图10-4

计算傅里叶系数为

因被积函数为偶函数，故

因此，函数f（t）的傅里叶级数为