使用极坐标系计算二重积分微积分

有的二重积分在直角坐标系中计算可能很困难，但当积分区域D的边界曲线采用极坐标方程来表示时，则较简单，如圆形或扇形区域的边界等，并且被积函数在极坐标系下表示也较简单，通常可考虑利用极坐标来计算二重积分.

在直角坐标系xOy中，取原点作为极坐标系的极点，x轴的正半轴为极轴（见图9-23），则点P的直角坐标（x，y）与极坐标（r，θ）有关系式

要在极坐标系中计算二重积分，需将被积函数f（x，y）和积分区域D以及面积元素dσ都用极坐标表示.

函数f（x，y）的极坐标形式容易求得，只要把变换公式x=r cosθ，y=r sinθ代入函数f（x，y），即得函数的极坐标形式f（r cosθ，r sinθ）.

下面讨论极坐标系下面积元素dσ的表达式.

设D的边界曲线与从极点O出发且穿过闭区域D内部的射线相交不超过两点，函数f（x，y）在D上连续.由于二重积分存在时，积分和式的极限与分割的方式无关.因此，此时不妨采用以极点为中心的一簇同心圆：r=常数，以及从极点出发的一簇射线：θ=常数，把区域D分割成许多小闭区域（见图9-24），设其中一个典型小闭区域Δσ（Δσ同时也表示该小闭区域的面积）是由半径分别为r，r+Δr的同心圆和极角分别为θ，θ+Δθ的射线所确定，则

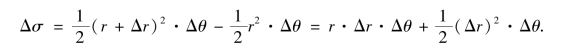
图9-23

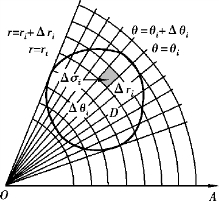
图9-24

当Δr和Δθ都充分小时，除去一个比Δr·Δθ高阶的无穷小，就得到Δσ的近似公式

于是，根据微元法可得到极坐标系下的面积元素

从而得到从直角坐标系变换为极坐标系下的变换公式

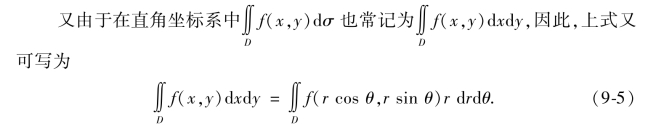
极坐标系中的二重积分，同样可化为二次积分来计算，下面分3种情况进行讨论，在讨论中假定所给函数在指定的区域上均连续.

（1）如果积分域D介于两条射线θ=α和θ=β之间，而对D内任一点（r，θ），其极径总是介于曲线r=φ1（θ）和r=φ2（θ）之间（见图9-25），则区域D的积分限

图9-25

于是

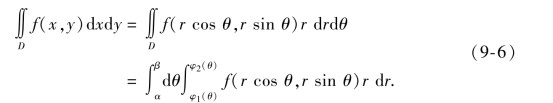
（2）如果积分区域D是如图9-26所示的曲边扇形，那么可把它看成图9-25中当φ1（θ）=0，φ2（θ）=φ（θ）时的特例.这时，闭区域D可表示为

于是

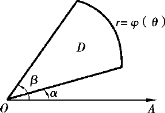
图9-26

图9-27

（3）如果积分区域D如图9-27所示，极点在D的内部，则可把它看成图9-26中当α=0，β=2π时的特例.这时，闭区域D可表示为

于是

注　根据二重积分的性质3，闭区域D的面积可表示为

特别地，如果闭区域D如图9-26所示，则有

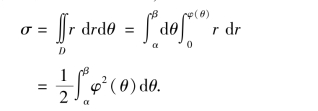
由上面的讨论不难发现，将二重积分化为极坐标形式进行计算，其关键在于：将积分区域D用极坐标变量r，θ表示为

下面通过具体例子来介绍如何在极坐标系下计算二重积分.

解　画出积分区域D，如图9-28所示.(www.xing528.com)

图9-28

在极坐标系下区域D表示为

所以

注　由于积分∫e-x2dx不能用初等函数表示，因此，此题在直角坐标系的两种积分次序都不可能计算出来.

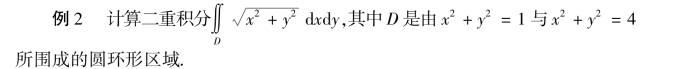
解　画出积分区域D，如图9-29所示.在极坐标系下区域D表示为

所以

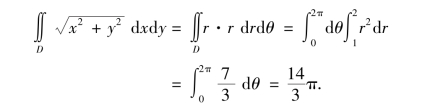
图9-29

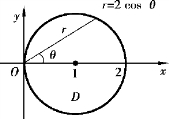
图9-30

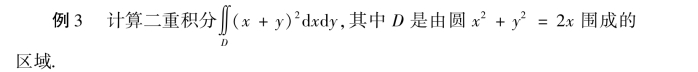
解　画出积分区域D，如图9-30所示.

圆x2+y2=2x的极坐标方程为r=2 cosθ，在极坐标系下区域D表示为

所以

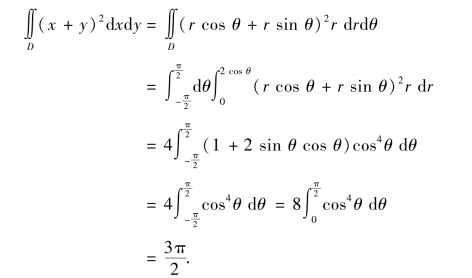
例4　计算积分

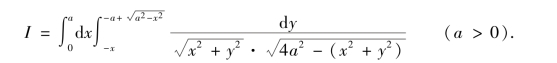
图9-31

解　积分区域D为

画出积分区域D，如图9-31所示.

在极坐标系下区域D表示为

所以

　例5　计算概率积分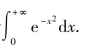

分析　这是一个广义积分，由于e-x2的原函数不能用初等函数表示，因此，利用广义积分无法计算.现利用二重积分来计算，其思想与一元函数的广义积分是一样的.

解　记

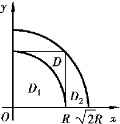
图9-32

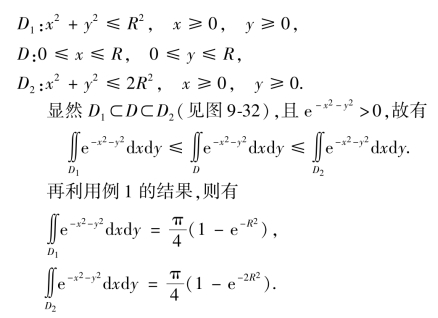
而

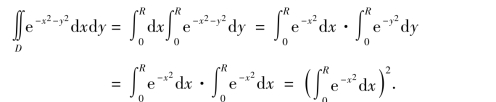
于是，不等式可改写为

所以

利用极坐标系求二重积分的值是计算二重积分的一种非常方便且有效的方法.当积分区域是圆域、环域、扇形区域或环扇形区域或者被积函数中含有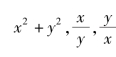等时，一般考虑用极坐标计算.