【摘要】:设xOy平面上的有界闭区域D可表示为其中,函数φ1(x),φ2(x)在区间[a,b]上连续,则称D为X型区域(见图9-6).图9-6X型区域的特点是:穿过D内部且垂直于x轴(或平行于y轴)的直线与D的边界相交不多于两个交点.下面借助几何直观地导出将二重积分转化为二次定积分的方法.设区域,若f(x,y)≥0且在D上连续,根据二重积分的几何意义可知,等于以D为底、以曲面z=f(x,y)为顶的曲顶柱体(
设xOy平面上的有界闭区域D可表示为
![]()
其中,函数φ1(x),φ2(x)在区间[a,b]上连续,则称D为X型区域(见图9-6).
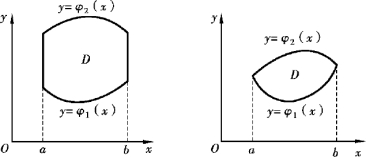
图9-6
X型区域的特点是:穿过D内部且垂直于x轴(或平行于y轴)的直线与D的边界相交不多于两个交点.
下面借助几何直观地导出将二重积分转化为二次定积分的方法.
设区域![]() ,若f(x,y)≥0且在D上连续,根据二重积分的几何意义可知,
,若f(x,y)≥0且在D上连续,根据二重积分的几何意义可知,![]() 等于以D为底、以曲面z=f(x,y)为顶的曲顶柱体(见图9-7)的体积.
等于以D为底、以曲面z=f(x,y)为顶的曲顶柱体(见图9-7)的体积.
下面应用第5章中计算“平行截面面积为已知的立体体积”的方法来计算曲顶柱体的体积.
在区间[a,b]上任意取定一点x0,过该点作平行于yOz面的平面x=x0.此平面截曲顶柱体所得的截面是一个以区间[φ1(x0),φ2(x0)]为底,曲边是曲线z=f(x0,y)的曲边梯形(见图9-7中的阴影部分),此截面的面积A(x0)可用定积分计算为
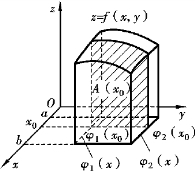
图9-7
![]() (https://www.xing528.com)
(https://www.xing528.com)
一般的,过区间[a,b]上任意一点x且平行于yOz面的平面截曲顶柱体所得截面的面积为
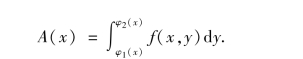
于是,曲顶柱体的体积为
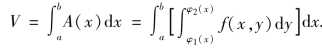
从而得到等式
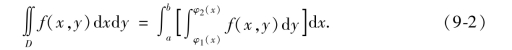
式(9-2)右端的积分称为先对y后对x的二次积分.就是说,先把x看成常数,把f(x,y)只看成y的函数,并对y计算在区间[φ1(x),φ2(x)]上的定积分.然后把算得的结果(不含y,是x的函数)再对x计算在区间[a,b]上的定积分.习惯上,常将式(9-2)右端的积分记作
![]()
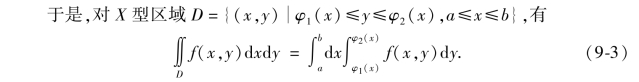
式(9-3)就是把二重积分化为先对y后对x的二次积分公式.
注 上述讨论中,假定f(x,y)≥0,但实际上式(9-3)的成立并不受此条件的限制.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




