微积分下册：曲顶柱体体积计算

设在空间直角坐标系中有一由闭合曲面所组成的立体，它的底是xOy面上的闭区域D，它的侧面是以D的边界曲线为准线而母线平行于z轴的柱面，它的顶是曲面z=f（x，y），其中f（x，y）≥0且在D上连续，这种立体称为曲顶柱体（见图9-1）.现要求这一曲顶柱体的体积.若z=f（x，y）取常数，此时的柱体为平顶柱体，它的体积可用公式

来计算.但对曲顶柱体，当点（x，y）在区域D上变化时，高度z=f（x，y）是一个变量，它的体积不能直接用上述公式来计算，可采用第5章中求曲边梯形的思路和方法来解决.

（1）大化小.用任意一组曲线网把D分成n个小闭区域

分别以这些小闭区域的边界曲线为准线，作母线平行于z轴的柱面，这些柱面把原来的曲顶柱体分为n个小曲顶柱体（见图9-2）.设第i个小曲顶柱体的体积为ΔVi（i=1，2，…，n），显然

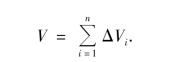
（2）常代变.当小区域Δσi（i=1，2，…，n）的直径（闭区域上任意两点间距离的最大值）很小时，因f（x，y）在D上连续，同一个小闭区域上的f（x，y）变化很小.这时，小曲顶柱体可近似看成平顶柱体.在每个小区域Δσi（小区域的面积也记作Δσi）中任取一点（ξi，ηi），则ΔVi近似等于以f（ξi，ηi）为高、以小区域Δσi为底的平顶柱体（见图9-2）的体积，即(www.xing528.com)

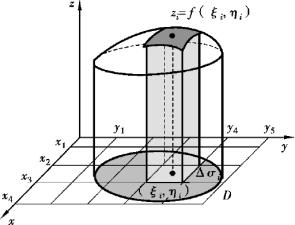
图9-2

（3）求和.将n个小平顶柱体体积相加，即得曲顶柱体体积的近似值为

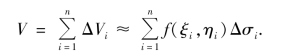
（4）取极限.记λ为n个小闭区域Δσi的直径的最大值，λ越小表示区域D分割越细.当λ→0时，上述和式的极限就是所求的曲顶柱体的体积V，即