微积分（下册）-解决线性规划问题

求多个自变量的线性函数在一组线性不等式约束条件下的最大值、最小值问题，是一类完全不同的问题，这类问题称为线性规划问题.下面通过实例来说明.

例2　一份简化的食物由粮和肉两种食品做成，每份粮价值30分，其中含有4单位碳水化合物，5单位维生素和2单位蛋白质；每份肉价值50分，其中含有1单位碳水化合物，4单位维生素和4单位蛋白质.对一份食物的最低要求是它至少要由8单位碳水化合物、20单位维生素和10单位蛋白质组成，问应选择什么样的食物，才能使价钱最便宜？

解　设食物由x份粮和y份肉组成，其价钱为

由食物的最低要求得到3个不等式约束条件，即：

为了有足够的碳水化合物，应有4x+y≥8；

为了有足够的维生素，应有5x+4y≥20；

为了有足够的蛋白质，应有2x+4y≥10；

并且还有x≥0，y≥0.

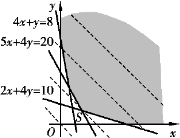
图8-30

上述5个不等式把问题的解限制在平面上如图8-30所示的阴影区域中，现在考虑直线簇C=30x+50y.当C逐渐增加时，与阴影区域相交的第一条直线是通过顶点S的直线，S是两条直线5x+4y=20和2x+4y=10的交点.因此，点S对应于C的最小值的坐标是，即这种食物是由份粮和份肉组成.代入C=30x+50y，即得所要求的食物的最低价格为

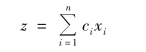
更一般的线性规划问题的提法是：求x1，x2，…，xn，使得

在m个不等式

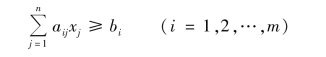
和(www.xing528.com)

的约束条件下取得最大值和最小值.在社会科学中，m=1 000，n=2 000的问题是很普遍的，这类问题一般用一些特殊的方法（如单纯形法）通过计算机来解决.

对两个或3个自变量的情形，也可用图形法（几何方法）来求解.下面的例子就是用几何方法来解决的.

例3　一个糖果制造商有500 g巧克力、100 g核桃和50 g果料.他用这些原料生产3种类型的糖果.A类每盒用3 g巧克力、1 g核桃和1 g果料，售价10元；B类每盒用4 g巧克力和1 g核桃，售价6元；C类每盒用5 g巧克力，售价4元.问每类糖果各应做多少盒，才能使总收入最大？

解　设制造商出售A，B，C 3类糖果各x，y，z盒，总收入R（元）是

不等式约束条件由巧克力、核桃和果料的存货限额给出，依次为

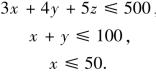
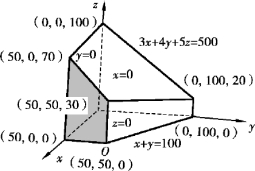
图8-31

当然，由问题的性质可知，x，y，z都是非负的，故x≥0，y≥0，z≥0.

于是，问题化为：求满足这些不等式的R的最大值.

上述不等式把允许的解限制在Oxyz空间中的一个多面体区域之内（见图8-31中变了形的盒子）.

在平行平面簇10x+6y+4z=R中只有一部分平面和这个区域相交，随着R增大，平面离原点越来越远.显然，R的最大值一定出现在这样的平面上，这种平面正好经过允许值所在多面体区域的一个顶点，所求的解对应于R取最大值的那个顶点，其计算结果列在表8-3中.

表8-3

由表8-3可知，R的最大值是920元，相应的点是（50，50，30），所以生产A类50盒，B类50盒，C类30盒时，收入最多.