微积分下册线性回归问题解析

通常许多工程问题需要根据两个变量的几组实验数值——实验数据，来找出这两个变量的函数关系的近似表达式.一般把这样得到的函数的近似表达式，称为经验公式.这是一种广泛采用的数据处理方法.经验公式建立后，就可把生产或实践中所积累的某些经验提高到理论上加以分析，并由此作出某些预测和规划.这里将利用本章所学知识进一步来探讨线性回归问题中回归直线的计算方法.

设n个数据点（xi，yi）（i=1，2，…，n）之间大致呈线性关系，则可设经验公式为

因为各个数据点并不在同一条直线上，所以只能要求选取这样的a和b，使y=ax+b在x1，x2，…，xn处的函数值与观测或试验数据y1，y2，…，yn相差都很小，就是要使偏差yi-（ai+b）（i=1，2，…，n）都很小，为了保证每个这样的偏差都很小，可考虑选取常数a和b，使

最小.这种根据偏差的平方和为最小的条件来选择常数a和b的方法，称为最小二乘法.

把M看成自变量a和b的一个二元函数，那么问题就归结为函数M=M（a，b）在哪些点处取得最小值的问题.令

整理得

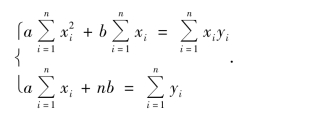
利用消元法，可直接解得

例1　为测定刀具的磨损速度，按每隔一小时测量一次刀具厚度的方式，得到表8-1的实测数据.

表8-1

(www.xing528.com)

试根据这组实测数据建立变量y和t之间的经验公式y=f（t）.

解　为确定f（t）的类型，利用所给数据在坐标纸上画出时间t和刀具厚度y的散点图（见图8-29）.

图8-29

观察此图易知，所给函数y=f（t）可近似看成线性函数，因此可设

其中，a和b是待定系数.由式（8-30）得

于是，所求经验公式为

表8-2