微积分（下册）：梯度概念详解

定义2　设函数z=f（x，y）在平面区域D内具有一阶连续偏导数，则对每一点P（x，y）∈D，都可定义一个向量

称它为函数z=f（x，y）在点P（x，y）处的梯度，记为grad f（x，y），即

如果函数f（x，y）在任一点P可微分，e=（cosα，cosβ）是与方向l同方向的单位向量，则根据方向导数的计算公式，有

其中，θ=（grad f（x，y），^e）表示向量grad f（x，y）与e的夹角.

这一关系式表明了函数在一点的梯度与函数在这点的方向导数间的关系，且就是梯度在射线l上的投影（见图8-28）.如果方向l与梯度方向一致时，有cos（grad f（x，y），^e）=1，即函数f沿梯度方向时，方向导数取得最大值，这个最大值就是梯度的模；如果方向l与梯度方向相反时，有cos（grad f（x，y），^e）=-1，即函数f沿梯度的反方向时，方向导数取得最小值.

图8-28

因此，有以下结论：

函数在某点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值.

根据梯度的定义，梯度的模为

当fx不为零时，x轴到梯度的转角的正切为

若fx，fy不同时为零，则等值线f（x，y）=c上任一点P0（x0，y0）处的一个单位法向量为

函数在一点的梯度方向与等值线在该点的一个法线方向相同，它的指向为从数值较低的等值线指向数值较高的等值线，而梯度的模等于函数在这个法线方向的方向导数.

梯度概念可推广到三元函数的情形.设函数u=f（x，y，z）在空间区域G内具有一阶连续偏导数，可类似地定义u=f（x，y，z）在G内点P（x，y，z）处的梯度为

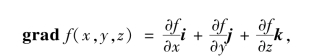
结论　三元函数的梯度也是一个向量，它的方向与取得最大方向导数的方向一致，其模为方向导数的最大值.

如果引进曲面f（x，y，z）=c为函数的等量面的概念，则可得函数u=f（x，y，z）在点P0（x0，y0，z0）的梯度的方向与过点P0的等量面f（x，y，z）=c在该点的法线的一个方向相同，且从数值较低的等量面指向数值较高的等量面，而梯度的模等于函数在这个法线方向的方向导数.

所以

例5　设f（x，y，z）=x2+y2+z2，求gradf（1，-1，2）.

解　(www.xing528.com)

于是

例6　函数u=xy2+z3-xyz在点P0（1，1，1）处沿哪个方向的方向导数最大？最大值是多少？

解　由，得

从而

　于是，u在点P0处沿方向（0，1，2）的方向导数最大，最大值是

数量场与向量场：如果对空间区域G内的任一点M，都有一个确定的数量f（M），则称在该空间区域G内确定了一个数量场（如温度场、密度场等）.一个数量场可用一个数量函数f（M）来确定.如果与点M相对应的是一个向量F（M），则称在该空间区域G内确定了一个向量场（如力场、速度场等）.一个向量场可用一个向量函数F（M）来确定，而

其中，P（M），Q（M），Q（M）是点M的数量函数.

利用场的概念，可以说向量函数grad f（M）确定了一个向量场——梯度场，它是由数量场f（M）产生的.通常称函数f（M）为这个向量场的势，而这个向量场又称势场.必须注意，任意一个向量场不一定是势场，因为它不一定是某个数量函数的梯度场.

解

同理

从而

梯度运算满足以下运算法则：设u，v可微，α，β为常数，则：

（1）grad（αu+βv）=agradu+βgradv.

（2）grad（u·v）=ugradv+vgradu.

（3）gradf（u）=f′（u）gradu.

以上性质请读者自证.