函数方向导数与梯度的应用

已知，二元函数z=f（x，y）的偏导数fx与fy能表达函数沿x轴与y轴的变化率，但仅知道这一点，在实际应用中是不够的.

例如，设有一块长方形的金属板，在一定的温度条件作用下，金属板受热产生了不均匀的稳定温度场，如图8-26所示.

图8-26

设在金属板中某处有一只蚂蚁，问这只蚂蚁在其逃生路线上的每一点处应沿什么方向逃生才能在最短时间内爬行到安全的地方？这个问题的答案是明显的，即这只蚂蚁在每一点处都应沿温度（下降）变化率最大的方向爬行.这个方向就是后面将要介绍的梯度的方向.

在物理学、仿生学和工程技术领域中，常常会遇到求函数沿某个方向的变化率问题.为此，引入函数的方向导数的概念.

定义1　设函数z=f（x，y）在点P（x，y）的某一邻域U（P）内有定义，l为自点P出发的射线，P′（x+Δx，y+Δy）为射线l上且含于U（P）内的任一点，以

表示点P与P′之间的距离（见图8-27）.如果极限存在，则称此极限值为函数f（x，y）在点P处沿方向l的方向导数，记为，即

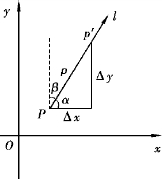
图8-27

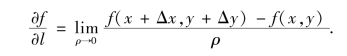
定理1　如果函数z=f（x，y）在点P（x，y）可微分，则函数在该点处沿任一方向l的方向导数都存在，且

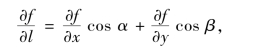
其中，cosα，cosβ是方向l的方向余弦.

证明　设Δx=ρcosα，Δy=ρcosβ，函数z=f（x，y）在点P（x，y）可微分，故该函数的增量可表示为

两边各除以ρ，得

故

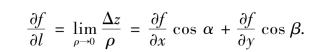
例1　求函数z=xe2y在点P（1，0）沿从点P（1，0）到点Q（2，-1）方向的方向导数.

因函数可微分，且

(www.xing528.com)

故所求方向导数为

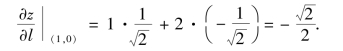
类似地，可定义三元函数u=f（x，y，z）在空间一点P（x，y，z）沿着方向l的方向导数为

其中，ρ为P（x，y，z）与点P′（x+Δx，y+Δy，z+Δz）之间的距离，即

设方向l的方向角为α，β，γ，则有

于是，当函数f（x，y，z）在P（x，y，z）处可微分时，函数在该点处沿任意方向l的方向导数都存在，且有

例2　求f（x，y，z）=xy+yz+zx在点（1，1，2）沿方向l的方向导数，其中l的方向角分别为60°，45°，60°.

解　与l同向的单位向量为

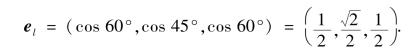
因为函数可微分，且

所以方向导数为

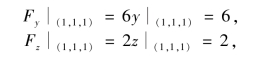
从而

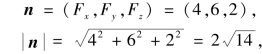
其方向余弦为.又

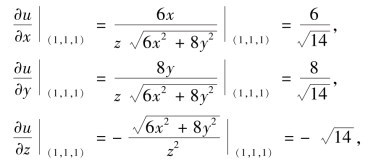
所以

在一个数量场中，函数在给定点处沿不同的方向，其方向导数一般是不相同的.现在我们所关心的是，沿哪一个方向其方向导数最大？其最大值是多少？为此引进一个很重要的概念——梯度，即函数在点P沿哪一方向增加的速度最快.