微积分（下册）：空间曲面的切平面及法线

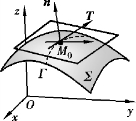
图8-25

（1）设曲面Σ的方程为M0（x0，y0，z0）是曲面Σ上的一点，函数F（x，y，z）的偏导数在该点连续且不同时为零.过点M0在曲面上可作无数条曲线.设这些曲线在点M0处分别都有切线，要证明这无数条曲线的切线都在同一平面上.

在曲面Σ上，过点M0任意作一条曲线Γ（见图8-25）.设曲线Γ的方程为

且t=t0时，对应于点M0（x0，y0，z0），即

由于曲线Γ在曲面Σ上，因此有

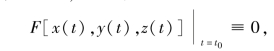
及

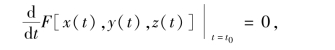
即有

　注意到曲线Γ在点M0处的切向量T=（x′（t0），y′（t0），z′（t0）），如果引入向量

则式（8-28）可写为

这说明曲面Σ上过点M0的任意一条曲线的切线都与向量n是垂直的，这样就证明了过点M0的任意一条曲线在点M0处的切线都落在以向量n为法向量且经过点M0的平面上.这个平面称为曲面Σ在点M0处的切平面.该切平面的方程为

曲面的法向量：垂直于曲面上切平面的向量，称为曲面的法向量.于是，在点M0的处曲面的法向量为

曲面的法线：过点M0（x0，y0，z0）且垂直于切平面的直线，称为曲面在该点的法线.法线方程为

（2）设曲面Σ的方程为

令F（x，y，z）=z-f（x，y），则有

于是，当函数f（x，y）的偏导数fx（x，y），fy（x，y）在点（x0，y0）处连续时，曲面Σ在点M0处的法向量为

从而切平面方程为

或

法线方程为

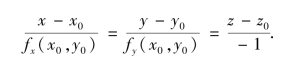
注　方程（8-29）的右端恰好是函数z=f（x，y）在点（x0，y0）处的全微分，而左端是切平面上点的竖坐标的增量.因此，函数z=f（x，y）在点（x0，y0）处的全微分，在几何上表示曲面z=f（x，y）在点（x0，y0）处的切平面上点的竖坐标的增量.

设α，β，γ表示曲面的法向量的方向角，并假定法向量与z轴正向的夹角γ是一锐角，则法向量的方向余弦为

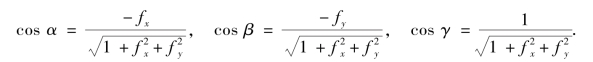
其中(www.xing528.com)

例4　求球面x2+y2+z2=14在点（1，2，3）处的切平面及法线方程.

解　令F（x，y，z）=x2+y2+z2-14，则

于是，球面在点（1，2，3）的法向量为　

所求切平面方程为

即

法线方程为

例5　求旋转抛物面z=x2+y2-1在点（2，1，4）处的切平面及法线方程.

解　令f（x，y）=x2+y2-1，于是法向量为

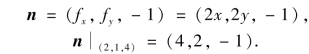
因此，在点（2，1，4）处的切平面方程为

即

法线方程为

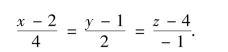
例6　求曲面x2+y2+z2-xy-3=0上同时垂直于平面z=0与x+y+1=0的切平面方程.

解　设F（x，y，z）=x2+y2+z2-xy-3，则

曲面在点（x0，y0，z0）处的法向量为

由于平面z=0的法向量n1=（0，0，1），平面x+y+1=0的法向量n2=（1，1，0），因为n同时垂直于n1与n2，所以n垂直于n1×n2，由

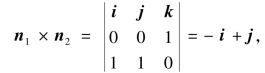
所以存在数λ，使得

即

解得x0=-y0，z0=0.将其代入题设曲面方程，得切点为

从而所求的切平面方程为

和