基础题
1.求下列函数的驻点，并判断是否为极值点（说明是极大值点，还是极小值点）.
（1）z=x2+y2. （2）z=（x-y+1）2. （3）z=x3+y3-3（x2+y2）.
2.求函数f（x，y）=4（x-y）-x2-y2的极值.
3.求函数f（x，y）=e2x（x+y2+2y）的极值.
4.求函数f（x，y）=x3+y3-9xy+27的极值.
5.求函数z=xy在条件x+y=1下的极大值.
6.将正数a分成3个正数之和，使它们的乘积为最大，求这3个正数.
提高题
1.【2003年数三】已知函数f（x，y）在点（0，0）的某邻域内连续，且
则下述4个选项中正确的是（ ）.
A.点（0，0）不是f（x，y）的极值点
B.点（0，0）是f（x，y）的极大值点
C.点（0，0）是f（x，y）的极小值点(www.xing528.com)
D.根据所给条件无法判断点（0，0）是否为f（x，y）的极值点
2.【2006年数一】设f（x，y）与φ（x，y）均为可微函数，且φ′y（x，y）≠0.已知（x0，y0）是f（x，y）在约束条件φ（x，y）=0下的一个极值点，下列选项正确的是（ ）.
3.【2011年数三】设函数f（x）具有二阶连续导数，且f（x）＞0，f′（0）=0，则函数z=f（x）ln f（y）在点（0，0）处取得极小值的一个充分条件是（ ）.
A.f（0）＞1，f″（0）＞0 B.f（0）＞1，f″（0）＜0
C.f（0）＜1，f″（0）＞0 D.f（0）＜1，f″（0）＜0
4.【2017年数一】已知函数y（x）由方程x3+y3-3x+3y-2=0确定，求y（x）的极值.
5.【2014年数一】设函数y=f（x）由方程y3+xy2+x2y+6=0确定，求f（x）的极值.
10.【2004年数一】设z=z（x，y）是由x2-6xy+10y2-2yz+18=0确定的函数，求z=z（x，y）的极值点和极值.
应用题
1.在平面x+z=0上求一点，使它到点A（1，1，1）和B（2，3，-1）的距离的平方和最小.
2.从斜边之长为l的一切直角三角形中，求有最大周长的直角三角形.
3.要造一个容积等于定数k的长方形无盖水池，应如何选择水池的尺寸，方可使它的表面积最小.
4.已知曲线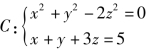
，求C上距离xOy面最远的点和最近的点.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
