微积分（下册）：二元函数极值

定义1　设函数z=f（x，y）在点（x0，y0）的某个邻域内有定义，如果对该邻域内任何异于（x0，y0）的点（x，y），都有

则称函数在点（x0，y0）处有极大值（或极小值）.极大值、极小值统称为极值.使函数取得极值的点称为极值点.

例1　函数z=2x2+3y2在点（0，0）处有极小值.当（x，y）=（0，0）时，z=0，而当（x，y）≠（0，0）时，z＞0，因此，z=0是函数的极小值.从几何上看，z=2x2+3y2表示一开口向上的椭圆抛物面，点（0，0，0）是它的顶点（见图8-20）.

例3　函数z=y2-x2在点（0，0）处既不取得极大值也不取得极小值，即在（0，0）处无极值.因为在点（0，0）处的函数值为零，而在点（0，0）的任一邻域内，总有使函数值为正的点，也有使函数值为负的点.从几何上看，它表示双曲抛物面（马鞍面）（见图8-22）.

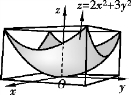
图8-20

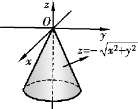
图8-21

图8-22

以上关于二元函数的极值概念，可推广到n元函数.设n元函数u=f（P）在点P0的某一邻域内有定义，如果对该邻域内任何异于P0的点P，都有

则称函数f（P）在点P0有极大值（或极小值）.

与导数在一元函数极值研究中的作用一样，偏导数也是研究多元函数极值的主要手段.

如果二元函数z=f（x，y）在点（x0，y0）处取得极值，那么固定y=y0，一元函数z=f（x，y0）在x=x0点处必取得相同的极值；同理，固定x=x0，z=f（x0，y）在y=y0点处也取得相同的极值.因此，由一元函数极值的必要条件，可得到二元函数极值的必要条件.

定理1（必要条件）　设函数z=f（x，y）在点（x0，y0）处具有偏导数，且在点（x0，y0）处有极值，则它在该点的偏导数必然为零，即

证明　不妨设z=f（x，y）在点（x0，y0）处有极大值.依极大值的定义，对点（x0，y0）的某邻域内异于（x0，y0）的点（x，y），都有不等式

特殊地，在该邻域内取y=y0而x≠x0的点，也应有不等式

成立.这表明一元函数f（x，y0）在x=x0处取得极大值，因而必有

同理，可证

类似地，如果三元函数u=f（x，y，z）在点P（x0，y0，z0）处具有偏导数，则它在点P（x0，y0，z0）处有极值的必要条件为

(www.xing528.com)

从几何上看，这时如果曲面z=f（x，y）在点（x0，y0，z0）处有切平面，则切平面

成为平行于xOy坐标面的平面z=z0.

仿照一元函数，凡是能使一阶偏导数同时为零，即fx（x0，y0）=0，fy（x0，y0）=0同时成立的点（x0，y0），称为函数z=f（x，y）的驻点.

注　根据定理1，具有偏导数的函数的极值点必定是驻点，但函数的驻点不一定是极值点.

例如，函数z=xy在点（0，0）处的两个偏导数都是零，即点（0，0）是函数z=xy的驻点，但函数在点（0，0）处既不取得极大值也不取得极小值.

如何判定一个驻点是否为极值点？下面的定理部分地回答了这个问题.

定理2（充分条件）　设函数z=f（x，y）在点（x0，y0）的某邻域内连续且有一阶及二阶连续偏导数，又fx（x0，y0）=0，fy（x0，y0）=0.令

则函数z=f（x，y）在点（x0，y0）是否取得极值的条件如下：

（1）AC-B2＞0时具有极值，且当A＞0时有极小值f（x0，y0）；当A＜0时有极大值f（x0，y0）.

　（2）AC-B2＜0时没有极值.

（3）AC-B2=0时可能有极值，也可能没有极值.

注　在定理2中，如果AC-B2=0，则不能确定f（x0，y0）是否是极值，需另作讨论.

根据定理1与定理2，若函数f（x，y）具有二阶连续偏导数，则求z=f（x，y）的极值的一般步骤如下：

（1）解方程组fx（x0，y0）=0，fy（x0，y0）=0，求出f（x，y）的所有驻点.

（2）求出函数f（x，y）的二阶偏导数，依次确定各驻点处A，B和C的值.

（3）根据AC-B2的正负号判定驻点是否为极值点，最后求出函数f（x，y）在极值点处的极值.

例4　求函数f（x，y）=x3-y3+3x2+3y2-9x的极值.

解　解方程组

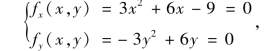
求得x=1，-3；y=0，2.于是，得驻点为（1，0），（1，2），（-3，0），（-3，2）.

再求出二阶偏导数

在点（1，0）处，AC-B=12×6＞0，又A＞0，故函数在点（1，0）处有极小值f（1，0）=-5.

在点（1，2），（-3，0）处，AC-B2=-12×6＜0，故函数在这两点处没有极值.

在点（-3，2）处，AC-B2=-12×（-6）＞0，又A＜0，故函数在点（-3，2）处有极大值f（-3，2）=31.

注　在讨论一元函数的极值问题时，已知函数的极值点既可能在驻点处取得，也可能在导数不存在的点处取得.同样，多元函数的极值也可能在个别偏导数不存在的点处取得.例如，函数在点（0，0）处有极大值，但函数在点（0，0）处不存在偏导数，点（0，0）也就不是函数的驻点.因此，在考虑函数的极值问题时，除了考虑函数的驻点外，还要考虑那些使偏导数不存在的点.