在一元微分学中,曾引入了隐函数的概念,并介绍了不经过显化而直接由方程F(x,y)=0来求它所确定的隐函数的导数的方法.这里将进一步从理论上阐明隐函数的存在性,并通过多元复合函数求导的链式法则,建立隐函数的求导公式,给出一套所谓的“隐式”求导法.
将y=f(x)代入F(x,y)=0,得恒等式
利用复合求导法则在上述方程两端对x求导,得
由于Fy连续,且Fy(x0,y0)≠0,因此,存在(x0,y0)的一个邻域,在这个邻域内Fy≠0,于是得
整理可得以下定理:
隐函数存在定理1:
设函数F(x,y)在点P(x0,y0)的某一邻域内具有连续偏导数,且F(x0,y0)=0,Fy(x0,y0)≠0,则方程F(x,y)=0在点P(x0,y0)的某一邻域内恒能唯一确定一个连续且具有连续导数的函数y=f(x),它满足条件y0=f(x0),并有
将式(8.17)两端视为x的函数,继续利用复合求导法则在上式两边求导,可求得隐函数的二阶导数
例1 验证方程x2+y2-1=0在点(0,1)的某一邻域内能唯一确定一个有连续导数,且当x=0时,y=1的隐函数为y=f(x),求该函数的一阶和二阶导数在x=0的值.
解 设F(x,y)=x2+y2-1,则
因此,由定理1可知,方程x2+y2-1=0在点(0,1)的某一邻域内能唯一确定一个有连续导数且当x=0时,y=1的隐函数为y=f(x).
下面再求该函数的一阶和二阶导数,即
隐函数存在定理还可推广到多元函数.一个二元方程F(x,y)=0可确定一个一元隐函数,一个三元方程F(x,y,z)=0可确定一个二元隐函数.
隐函数存在定理2:
设函数F(x,y,z)在点P(x0,y0,z0)的某一邻域内具有连续的偏导数,且F(x0,y0,z0)=0,Fz(x0,y0,z0)≠0,则方程F(x,y,z)=0在点P(x0,y0,z0)的某一邻域内恒能唯一确定一个连续且具有连续偏导数的函数z=f(x,y),它满足条件z0=f(x0,y0),并有
证明 将z=f(x,y)代入F(x,y,z),得
利用复合求导法则,在上式两端分别对x和y求导,得
因为Fz连续,且Fz(x0,y0,z0)≠0,所以存在点(x0,y0,z0)的一个邻域,在这个邻域内Fz≠0,于是得
例2 设x2+y2+z2-4z=0,求![]()
解 设F(x,y,z)=x2+y2+z2-4z,则(https://www.xing528.com)
利用隐函数存在定理2,得
注 在实际应用中,求方程所确定的多元函数的偏导数时,不一定非得套用公式,尤其是方程中含有抽象函数时,利用求偏导数或求微分的过程进行推导更为清楚.
例3 设z=f(x+y+z,xyz),求![]()
解 令u=x+y+z,v=xyz,则
把z看成x,y的函数对x求偏导数,得
所以
把x看成z,y的函数对y求偏导数,得
所以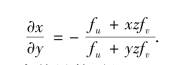
把y看成x,z的函数对z求偏导数,得![]()
所以
例4 设F(x-y,y-z,z-x)=0,其中F具有连续偏导数,且F′2-F′3≠0.求证:![]()
解 由题意知方程确定函数z=z(x,y).在题设方程两边求微分,得
即有
根据微分运算,得
合并同类项,得
两边同除以F′2-F′3,得
从而
于是
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




