【摘要】:定理3如果函数u=φ(x,y)在点(x,y)处具有对x及对y的偏导数,函数v=ψ(y)在点y处可导,函数z=f(u,v)在对应点(u,v)处具有连续偏导数,则复合函数z=f[φ(x,y),ψ(y)]在点(x,y)处的两个偏导数存在,且有在第三种情形中,一种常见的情况是:复合函数的某些中间变量本身又是复合函数的自变量的情形.例如,设函数z=f(u,x,y),u=φ(x,y)构成复合函数z=f[φ(
定理3 如果函数u=φ(x,y)在点(x,y)处具有对x及对y的偏导数,函数v=ψ(y)在点y处可导,函数z=f(u,v)在对应点(u,v)处具有连续偏导数,则复合函数z=f[φ(x,y),ψ(y)]在点(x,y)处的两个偏导数存在,且有


在第三种情形中,一种常见的情况是:复合函数的某些中间变量本身又是复合函数的自变量的情形.
例如,设函数z=f(u,x,y),u=φ(x,y)构成复合函数z=f[φ(x,y),x,y],其变量间的相互依赖关系如图8-19所示,则此类情形可视为第二种情形式(8-11)和式(8-12)中v=x,w=y的情况.从而有
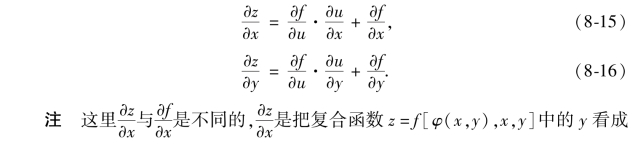

图8-19



例3 设z=uv+sin t,而u=et,v=cos t,求全导数![]()
解
 (https://www.xing528.com)
(https://www.xing528.com)
例4 设z=xy+u,u=φ(x,y),求![]()
解
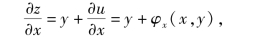

在多元函数的复合求导中,为了简便起见,常采用记号
![]()
其中,下标1表示对第一个变量u求偏导数,下标2表示对第二个变量v求偏导数.同理,有f″11,f″22等.
例5 设w=f(x+y+z,xyz),f具有二阶连续偏导数,求![]() 及
及![]()
解 令u=x+y+z,v=xyz,则w=f(u,v),根据复合求导法则,有

注

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




