【摘要】:与一元函数的极限概念类似,如果在P(x,y)→P0(x0,y0)的过程中,对应的函数值f(x,y)无限接近于一个确定的常数A,则称A是函数f(x,y)当(x,y)→(x0,y0)时的极限.定义2设二元函数z=f(x,y)在点P(x0,y0)的某一去心邻域D内有定义,如果对任意给定的正数ε,总存在正数δ,使得对满足不等式的一切点P(x,y)∈D恒有成立,则称常数A为函数f(x,y)当P(x,y)→
与一元函数的极限概念类似,如果在P(x,y)→P0(x0,y0)的过程中,对应的函数值f(x,y)无限接近于一个确定的常数A,则称A是函数f(x,y)当(x,y)→(x0,y0)时的极限.
定义2 设二元函数z=f(x,y)在点P(x0,y0)的某一去心邻域D内有定义,如果对任意给定的正数ε,总存在正数δ,使得对满足不等式
![]()
的一切点P(x,y)∈D恒有
![]()
成立,则称常数A为函数f(x,y)当P(x,y)→P0(x0,y0)时的极限.记为
![]()
也记作
![]()
为了区别于一元函数的极限,二元函数的极限也称二重极限.
例6 求极限![]()
解 令u=x2+y2,则
![]()

图8-11
必须注意:(https://www.xing528.com)
(1)二重极限存在,是指P以任何方式趋于P0时(见图8-11),函数都无限接近于A.
(2)如果当P以两种不同方式趋于P0时,函数趋于不同的值,则函数的极限不存在.

证明 当点P(x,y)沿x轴趋于点(0,0)时
![]()
当点P(x,y)沿y轴趋于点(0,0)时
![]()
当点P(x,y)沿直线y=kx有

易知,题设极限的值随k的变化而变化,故函数f(x,y)在(0,0)处极限不存在.
二元函数的极限与一元函数的极限具有相同的性质和运算法则,但洛必达法则不能延用.
例8 求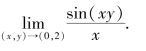
解

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




