微积分下册：二元函数概念

例1　圆柱体的体积V和它的底半径r、高h之间具有关系

例2　一定量的理想气体的压强p、体积V和绝对温度T之间具有关系

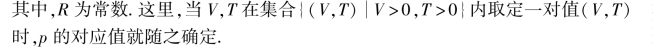
例3　设R是电阻R1，R2并联后的总电阻.由电学已知，它们之间具有关系

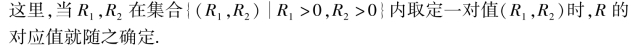
定义1　设D是平面R2上的一个非空点集，如果对D内的任一点（x，y），按照某种法则f，都有唯一确定的实数z与之对应，则称映射f：D→R为定义在D上的二元函数，通常记为

其中，x，y称为自变量，z称为因变量.点集D称为该函数的定义域，数集称为该函数的值域.

上述定义中，与自变量x，y的一对值（x，y）相对应的因变量z的值，也称f在点（x，y）处的函数值，记作f（x，y），即z=f（x，y）.

函数的其他符号有z=z（x，y），z=g（x，y）等.

类似地，可定义三元函数u=f（x，y，z），（x，y，z）∈D以及三元以上的函数.当n≥2时，n元函数统称为多元函数.

注　关于函数定义域的约定：如果一个用算式表示的函数没有明确指出定义域，则该函数的定义域理解为使算式有意义的所有点（x，y）所构成的集合，并称其为自然定义域.因此，对这类函数，它的定义域不再特别标出.例如：

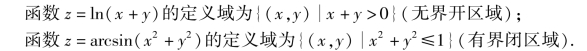
例4　求此二元函数的定义域

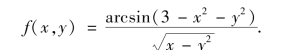
解　要使表达式有意义，必须

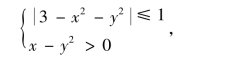
即

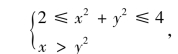(www.xing528.com)

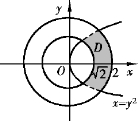
图8-7

故所求定义域为（见图8-7）

例5　已知函数，求f（x，y）.

解　设u=x+y，v=x-y，则

所以

即有

二元函数的几何意义：

二元函数的图形：点集称为二元函数z=f（x，y）的图形.易知，属于S的点P（x0，y0，z0）满足三元方程F（x，y，z）=z-f（x，y）=0，故二元函数z=f（x，y）的图形就是空间中区域D上的一张曲面（见图8-8），定义域D就是该曲面在xOy面上的投影.

例如，z=ax+by+c是一张平面，而函数z=x2+y2的图形是旋转抛物面.

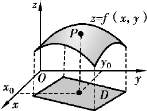
图8-8

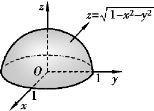
图8-9

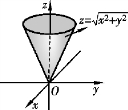
图8-10