微积分（下册）：平面区域的概念

在上册讨论一元函数时，一些概念、理论和方法都是基于一维实数点集、两点间的距离、区间和邻域等概念.为了将一元函数微积分推广到多元的情形，首先需要将上述概念加以推广，同时还需涉及一些其他概念.为此，先引入平面点集的一些基本概念，再将有关概念从一维的情形推广到二维及n维的情况.

由平面解析几何已知，当在平面上引入了一个直角坐标系后，平面上的点P与有序二元实数组（x，y）之间就建立了一一对应关系.于是，常把有序实数组（x，y）与平面上的点P视为等同的.这种建立了坐标系的平面，称为坐标平面.二元的有序实数组（x，y）的全体，即就表示坐标平面.

坐标平面上具有某种性质P的点的集合，称为平面点集，记作

例如，平面上以原点为中心、r为半径的圆内所有点的集合是

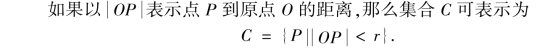
与数轴上邻域的概念类似，这里引入平面上点的邻域概念.

设P0（x0，y0）是xOy平面上的一个点，δ是某一正数.与点P0（x0，y0）距离小于δ的点P（x，y）的全体，称为点P0的δ邻域，记为U（P0，δ），即

或

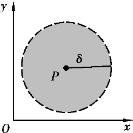
图8-1

邻域的几何意义：U（P0，δ）表示xOy平面上以点P0（x0，y0）为圆心、δ为半径的圆的内部点P（x，y）的全体（见图8-1）.

点P0的去心δ邻域，记作U°（P0，δ），即

注　如果不需要强调邻域的半径δ，则用U（P0）表示点P0的某个邻域，点P0的去心邻域记作U°（P0）.

下面利用邻域来描述平面上点和点集之间的关系.

设E是平面上的一个点集，P是平面上的一个点，则点P与点集E之间必有以下3种关系中之一：

（1）内点：如果存在点P的某个邻域U（P），使得U（P）⊂E，则称P为E的内点（见图8-2中的点P1）；

（2）外点：如果存在点P的某个邻域U（P），使得U（P）∩E=∅，则称P为E的外点（见图8-2中的点P2）；

（3）边界点：如果点P的任一邻域内既有属于E的点，也有不属于E的点，则称P点为E的边界点（见图8-2中的点P3）.

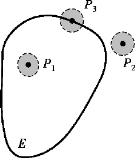
图8-2

点集E的边界点的全体，称为E的边界，记作∂E.

根据上述定义可知，点集E的内点必属于E，E的外点必定不属于E，而E的边界点则可能属于E，也可能不属于E.

如果按点P的邻近处是否有无穷多个点来分类，则有：(www.xing528.com)

（1）如果对任意给定的δ＞0，点P的去心邻域U°δ（P）内总有点集E中的点，则称P是E的聚点.

（2）设点P∈E，如果存在点P的某个去心邻域U°（P），使得U°（P）∩E=∅，则称P为E的孤立点.

由聚点的定义可知，点集E的聚点P本身，可能属于E，也可能不属于E.

例如，设平面点集

满足1＜x2+y2＜2的一切点（x，y）都是E的内点；满足x2+y2=1的一切点（x，y）都是E的边界点，它们都不属于E；满足x2+y2=2的一切点（x，y）也是E的边界点，它们都属于E；点集E以及它的界边∂E上的一切点都是E的聚点.

根据点集所属点的特征，可进一步定义一些重要的平面点集.

（1）开集：如果点集E内任意一点均为其内点，则称E为开集.例如

（2）闭集：如果点集E的余集E 为开集，则称E为闭集.例如

集合既非开集，也非闭集.

（3）连通性：如果点集E内任何两点，都可用折线连接起来，且该折线上的点都属于E，则称E为连通集（见图8-3）.

（4）区域（或开区域）：连通的开集称为区域或开区域.例如

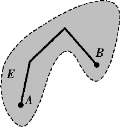
图8-3

（5）闭区域：开区域连同它的边界一起所构成的点集，称为闭区域.例如

（6）有界集：对平面点集E，如果存在某一正数r，使得E⊂U（O，r），其中O是坐标原点，则称E为有界点集.

（7）无界集：一个集合如果不是有界集，就称这集合为无界集.

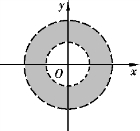
图8-4

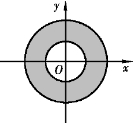
图8-5

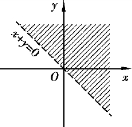
图8-6