【摘要】：图7-14所以得x-x0=tm，y-y0=tn，z-z0=tp，故直线方程为式（7-15）称为直线的点向式方程，又称直线的对称式方程或标准方程.其中，直线的任一方向向量s的坐标m，n，p，称为方向数；向量s的方向余弦，称为该直线的方向余弦.显然，与m，n，p成比例的任何一组（不全为零的）数均为同一直线的方向数.由直线的对称式方程容易导出直线的参数式方程.设得方程组式中，t是参变量.由于空间直线可看
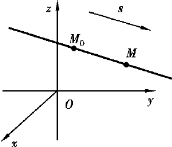
图7-14
所以得x-x0=tm，y-y0=tn，z-z0=tp，故直线方程为
式（7-15）称为直线的点向式方程，又称直线的对称式方程或标准方程.其中，直线的任一方向向量s的坐标m，n，p，称为方向数；向量s的方向余弦，称为该直线的方向余弦.显然，与m，n，p成比例的任何一组（不全为零的）数均为同一直线的方向数.
由直线的对称式方程容易导出直线的参数式方程.设
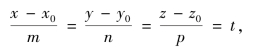
得方程组
式中，t是参变量.
由于空间直线可看成两个平面的交线，因此，直线的一般式方程为
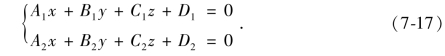(www.xing528.com)
式（7-17）又称直线的交面式方程.一般式方程为两平面的交线，所以两平面的法向量不能平行.通过空间一条直线的平面有无限多个，只要在这无限多个平面中任意选取两个，把它们的方程联立起来，所得的方程组就表示该空间直线了.
例5 已知不同的两点M1（x1，y1，z1）和M2（x2，y2，z2），求过这两点的直线方程.
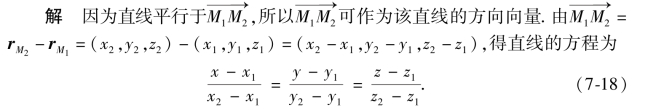
式（7-18）又称直线的两点式方程.
例6 已知直线的一般式方程为
，求此直线的对称式方程及参数方程.
解 先求直线上的一点.取x=1，有
解此方程组，得y=-2，z=0.即（1，-2，0）就是直线上的一点.
再求这直线的方向向量s.以平面x+y+z=1和2x-y+3z=4的法向量的向量积作为直线的方向向量s，则
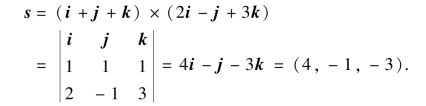
因此，所给直线的对称式方程为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
