递归(recursion)作为一种算法在程序设计语言中应用广泛。方法的递归调用是指方法在运行过程中直接或间接调用自身而产生的重入现象。递归调用必须要有结束条件,否则就会陷入无限递归的状态,永远无法结束。
递归通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
可见,构成递归需具备的条件:
(1)子问题须与原始问题为同样的事,且更为简单;
(2)不能无限制地调用本身,必须有个出口,化简为非递归状况处理。
递归调用的方式包括直接调用和间接调用。直接调用的语法格式为:

间接调用的语法格式为:

【例2-20】
利用递归方式计算从1加到100的和。
分析:采用递归调用的难点在于递归算法的设计。本例中,抽象出如下递归算法:
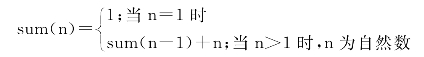
要计算sum(n),根据公式要先计算sum(n-1),这就是递归调用,算法相同但是参数值不同。同样,为了计算sum(n-1),要调用自身算法先计算sum(n-2),……,为了计算sum(2),要先计算sum(1),而sum(1)的值是已知的,即为递归出口,然后逐级返回,先得到sum(2)的值,接着得到sum(3)的值,……,最后得到sum(n)。
程序实现如图2-36所示。(https://www.xing528.com)

图2-36 方法递归调用示例
本例的递归算法,每调用自身一次,参数n的值就减1,离递归结束条件就更近一步,当参数n减少到1时到达边界,满足递归结束条件,接着,所有递归调用的方法都以相反的顺序相继结束,最终得到sum(n)的计算结果。
采用递归算法实现的方法每调用一次都会在栈顶产生一个栈帧。本例中,递归调用时虚拟机栈中栈帧分配如图2-37所示。

图2-37 递归调用时栈帧分配
当满足递归结束条件时,栈帧又依次弹出,递归调用的方法依次返回结果,最终得到sum(100)的计算结果。
栈是用来存储方法调用信息的绝好方案,这归功于其后进先出的特点满足了方法调用和返回的顺序。然而,使用栈也有一些缺点。
(1)栈维护了每个方法调用的信息直到方法返回后才释放,占用空间大,尤其是在程序中递归调用很多的情况下。
(2)因有大量的信息需保存和恢复,故生成和销毁活跃记录需要耗费一定的时间。
关于递归的使用,还有以下两点提示:
(1)尽量不要使用层次较深的递归调用。
(2)关于递归与循环的转化问题。有的递归可以通过循环实现,例如本例,之前通过for循环实现,再比如,求阶乘数n!,可以采用递归,也可以采用循环实现。当然,很多时候很难用循环来替代,此时递归调用是必需的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




