大学物理实验教程：最小二乘法

根据前面介绍,作图法或逐差法都可以用来确定两个物理量之间的定量函数关系。然而,两者也都存在着某些缺点和限制。不同的人用相同的实验数据作图,由于主观随意性,拟合出的直线(或曲线)往往是不一致的,因此通过斜率或截距计算的结果也是不同的,逐差法也受到函数形式和自变量变化要求的限制,且两种方法的精度都较低。相比而言,最小二乘法是更严格、精度更高的一种数据处理方法。

最小二乘法是回归分析法的重要环节,是建立在数理统计理论基础之上的一种方法,被广泛地应用在工程和实验技术等方面。一个完整的回归分析过程应包括回归方程的假设、方程系数的确定、回归方程合理性分析和检验等三个环节。限于本课程教学要求,在此只讨论如何用最小二乘法确定方程中的系数,而且只讨论一元线性函数。

1)最小二乘原理

所谓最小二乘原理,就是在满足各测量误差平方和最小的条件下得到的未知量值为最佳值。用公式表示为

最小二乘中的“二”指的是平方。

2)用最小二乘法进行线性拟合

设已知函数形式为

在等精度测量条件下得到一组测量数据为

x1,x2,…,xn

y1,y2,…,yn

由此得到n个观测方程

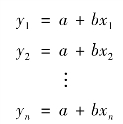
一般情况下,观测方程个数大于未知量的数目时,a、b的解不确定。因此,如何从这n个观测方程中确定出a、b的最佳值,或者说如何从以xi、yi(i=1,2,…,n)为实验点画出的直线中确定出最佳直线是关键问题。使用最小二乘法可以解决这个问题。

假定最佳直线方程为

式中,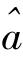和为直线方程的最佳系数。为了简化,设测量中x方向的误差远小于y方向的,可以忽略,只研究y方向的差异,则有

根据最小二乘原理,系数的最佳值应满足

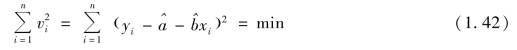
要使上式成立,显然应有(www.xing528.com)

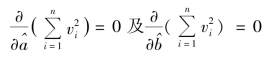
将代入,整理后得以下两个方程

或

式中,为x的算术平均值;为y的算术平均值;为x2的算术平均值;为xy的算术平均值。

求解方程组(1.44)得

由所确定的方程即是最佳直线方程。

3)最小二乘法应用举例

例1.9　根据例1.7数据,试用最小二乘法确定关系式R=a+bt。

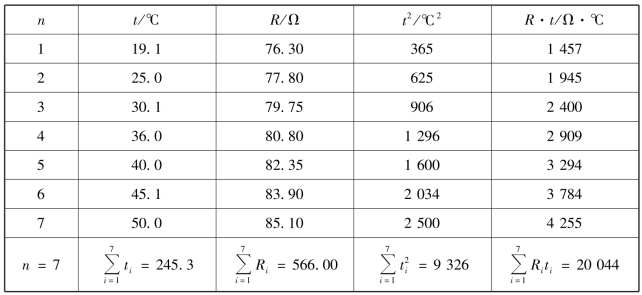
解:①由表1.5算出

②由表1.6可得

a、b的最佳值为

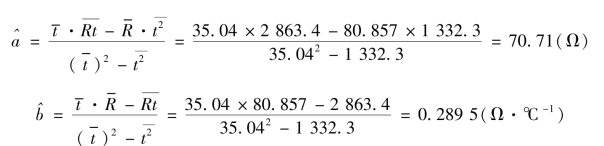
表1.6　最小二乘法处理数据表

③待求关系式

R=(70.71+0.289 5t)Ω