大学物理实验教程：作图法-连线方法与应用举例

(1)作图法的优点

①能够直观地反映各物理量之间的变化规律,帮助找出合适的经验公式。

②可从图上用外延、内插方法求得实验点以外的其他点。

③可以消除某些恒定系统误差。

④具有取平均、减小随机误差的作用。

⑤通过作图还可以对实验中出现的粗大误差做出判断。

(2)作图规则

①根据各量之间的变化规律,选择相应类型的坐标纸,如毫米直角坐标纸、双对数坐标纸、单对数坐标纸等;坐标纸的大小要适中,一般应根据测量数据的有效数字来确定。

②正确选择坐标比例,使图线能均匀位于坐标纸中间;两坐标轴的交点可以不为零。

③写明图名及各坐标轴所代表的物理量、单位和数值的数量级。

④用削尖的铅笔把对应的数据标在图纸上,描点应采用“×”“△”“○”等比较明显的标识符号。

⑤对变化规律容易判断的曲线以平滑线连接,曲线不必通过每个实验点,各实验点应均匀分布在曲线两边;难以确定规律的曲线可以用折线连接。图1.7和图1.8给出了两种不同连线方法的例子。

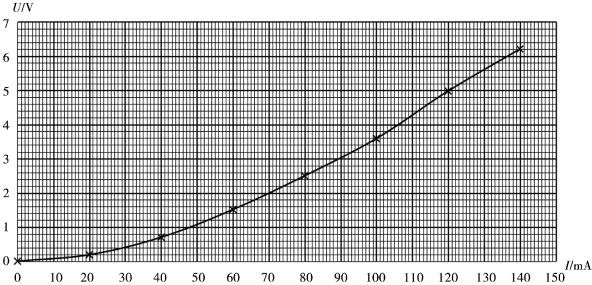
图1.7　按平滑规律变化连线(小灯泡伏安特性曲线)

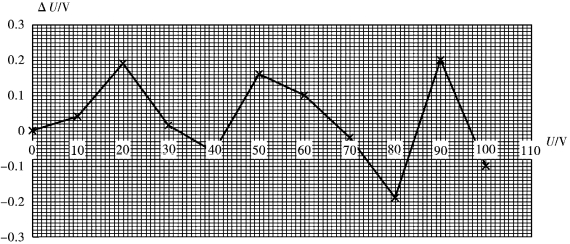
图1.8　按折线规律变化连线(电压表校准曲线)

(3)作图法的应用

作图法的应用主要表现在以下两方面。

1)判断各量的相互关系——图示法

通过作图可以判断各量的相互关系,特别是在还没有完全掌握科学实验的规律情况下,或还没有找出合适的函数表达式时,作图法是找出函数关系式并求得经验公式的最常用的方法之一。如二极管的伏安特性曲线、电阻的温度变化曲线等,都可通过作图清楚地表示出来。

2)图上求未知量——图解法

①从直线上求物理量

线性关系的函数中未知量往往包含在斜率和截距之中。例如,匀速直线运动s=s0+vt,若作s-t直线,其斜率就是速度,截距为运动物体的初始位置。因此,从直线上可以通过求斜率和截距来获取未知量。

求斜率时要在图中接近实验范围的两端,从直线上取两点(x1,y1)和(x2,y2),一般应避免使用实验点,则斜率为

截距的求法是:把图线延长到x=0时,y的值即为截距。如果x坐标轴的起点不为零,则利用图线上第三点的数据(x3,y3),代入公式y=a+kx求出,即(www.xing528.com)

②非线性函数中未知量的求法——曲线改直问题

物理实验中经常遇到的图线类型见表1.3。由于直线是最能够精确绘制的图线,因而总希望通过坐标代换将非直线变成直线。这被称为曲线改直技术。

如表1.3单摆的摆动一例中,单摆的摆长L随周期T的变化关系,具有y=axb形式(a、b为常量)。若观测单摆的周期T随摆长L的变化,得到一系列数据(Ti,Li)(i=1,2,…,n),如果在直角坐标纸上画出L-T曲线,则得到一条抛物曲线;如用L作纵轴,T2作横轴,结果将得到一条通过原点的直线,其斜率等于g/(4π2),从图上求出斜率后,可以计算出实验所在地的重力加速度。

表1.3　常见图线类型

对上述y=axb函数形式,也可以将方程两边取对数(以10为底),得到

lg y=b·lg x+lg a

在直角坐标纸上,以lg y为纵坐标,lg x为横坐标作图,可得到一条直线,从而可以求出系数a和b。

再如,电容器的放电过程,具有y=A eBx形式,A、B为常数。对这种形式的函数,两边取对数得到

ln y=Bx+ln A

显然,ln y和x具有线性关系,在直角坐标纸上呈现一条直线。通过求斜率和截距可以求出常数A和B。对于其他较为复杂的关系式,也可用类似的方法处理。读者若有兴趣,可以参考数据处理方面的专著。

③作图举例

例1.7　为确定电阻随温度变化的关系式,测得不同温度下的电阻值见表1.4,试用作图法作出R-t曲线,并确定关系式R=a+bt。

解:选用直角坐标纸作图,横坐标表示温度,最小刻度为1.0℃;纵坐标表示电阻R,最小刻度为0.1Ω,如图1.9所示。

表1.4　R-t对应数值表

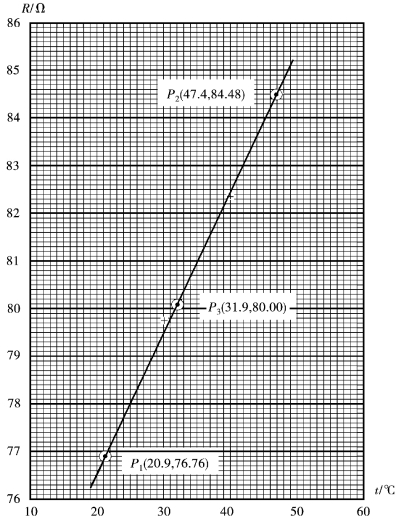
图1.9　典电阻随温度变化曲线

在图中任选两点P1(20.9,76.76)和P2(47.4,84.48),由公式(1.34)得到斜率

由于图中无t=0点,将第三点P3(31.9,80.00)代入公式(1.35)得到截距

a=80.00-0.291×31.9=70.72Ω

因此电阻与温度的关系为

R=70.72+0.291t