大学物理实验教程：处理随机误差

(1)随机误差的分布及其数字特征

1)正态分布及特点

尽管单次测量时随机误差的大小与正负是不确定的,但对多次测量来说却服从一定的统计规律。随机误差的统计分布规律有很多,正态分布是最常见的分布之一。

服从正态分布的随机误差的概率密度函数为或

式中,x为测量值;x0为真值;δ为误差;f表示在δ(或x)附近单位区间内,被测量误差(或测量值)出现的概率。分布曲线如图1.2所示。

由图1.2可以看出,正态分布的随机误差具有以下特点:

①单峰性:绝对值小的误差比绝对值大的误差出现的机会多;

②对称性(抵偿性):大小相同,符号相反的误差出现的机会相同;

③有界性:非常大的正误差或负误差出现的可能性几乎为零。

2)数字特征

数学期望与方差是定量描述统计规律分布的两个重要参数。根据式(1.5a)或式(1.5b),满足正态分布的随机变量δ或x,其数学期望为

或

上式说明,对于无限次测量,测量值的数学期望等于真值,或误差的数学期望等于零,即随机误差具有抵偿性。

根据式(1.5a)或式(1.5b),满足正态分布的随机变量δ或x,方差D及标准差σ为

或

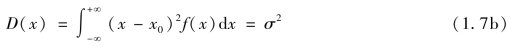
标准差

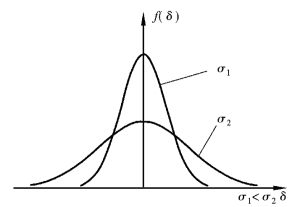
方差与标准差反映测量值与真值的偏离程度,或各测量值之间的离散程度。标准差或方差越小,离散程度越小,测量的精密度高;反之,离散程度越大。如图1.3所示。

图1.2　正态分布曲线

(www.xing528.com)

图1.3　σ对曲线的影响

标准差σ的物理意义也可以从下面这一角度理解:

根据概率密度函数的含义,误差出现在[δ,δ+dδ]范围内的概率为f(δ)dδ,则误差出现在区间[-σ,σ]内的概率为

上式表示,在一组测量数据中,有68.3%的数据测量误差落在区间[-σ,σ]内。也可以认为,任一测量数据的误差落在区间[-σ,σ]内的概率为68.3%。把P称为置信概率,而[-σ,σ]为68.3%的置信概率所对应的置信区间。

更广泛地,置信区间可由[-kσ,kσ]表示,k称为包含因子(或置信因子),可根据需要选取不同大小的值。例如,除了上述k=1的情况,还经常取k=2或3,这时的置信区间分别为[-2σ,2σ]和[-3σ,3σ],对应的置信概率为95.5%和99.7%。

可以看出,如果置信区间为[-3σ,3σ],则测量误差超出该区间的概率很小,只有0.3%,即进行1 000次测量,只有3次测量误差可能超出[-3σ,3σ]。对于有限次测量(次数少于20次),超出该区间的误差可以认为不会出现,因此常将±3σ称为极限误差。

(2)算术平均值与标准偏差

对真值为x0的某一量x做等精度测量,得到一测量列x1～xn,则该测量列的算术平均值为

若测量数据中无系统误差和粗大误差存在,由正态分布随机误差的对称性特点和数学期望、标准差含义可知,在测量次数n→∞时,有算术平均值

测量列标准差

在实际测量中,测量次数总是有限的,且真值不可知。因此,对于等精度测量列,可以用算术平均值作为真值的最佳估计值。而测量列标准差也需通过估计获得。估计标准差的方法很多,最常用的是贝塞尔法,即子样标准差。其公式为

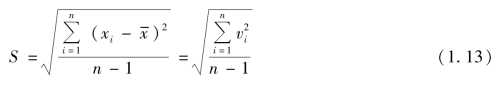
式中,vi=xi-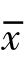称为残差。

由于算术平均值也是一个随机变量,进行多组等精度重复测量时得到的算术平均值具有离散性。描述该离散性的参数是算术平均值的标准差,由误差理论可以证明,算术平均值标准差与测量列(或单次测量)标准差之间的关系为

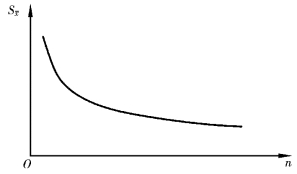
图1.4　测量次数对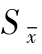的影响

由式(1.14)可看出,平均值的标准差比单次测量的标准差小。随着测量次数的增加,平均值的标准差越来越小,测量精密度越来越高。但当测量次数n>10以后,次数对平均值标准差的降低效果很小,如图1.4所示。所以,不能单纯通过增加次数来提高测量精度。在科学研究中测量次数一般取10～20次,而在大学物理实验中一般取5～10次。

当测量次数有限时,根据式(1.13)与式(1.14),算术平均值的标准差可由下式进行估计

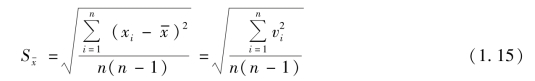
本书中采用式(1.15)来计算直接测量量的标准差。