数学艺术：极限为1的序列和以圆周率为极限的序列

序列与曙光

与前辈同胞毕达哥拉斯一样,欧几里得在数学之外也有许多爱好,他喜欢天文学、力学和音乐,可谓是多才多艺。据说欧几里得写过一本音乐的书,可惜没有流传下来。不过,欧几里得的著作《光学》却幸运地传了下来,其中的光学理论包含了透视的数学原理。事实上,这本书是最早的希腊文本的透视学。与他的《原本》一样,这本书的开头也列举了公设,总共12个,比《原本》(公设和公理各五个)还多两个,由此他推出61个命题。例如,公设一说的是:

人看见物体,是光线从眼睛出发射到所看见的物体上去。

阿拉伯数学家海桑

这是柏拉图以来的传统观点,后来却被巴士拉(今伊拉克)出生、有着“托勒密第二”雅号的阿拉伯人海桑(Alhazen, 965—1040)给否定掉了。海桑写过一本《光学》,后来被牛顿誉为最具影响力的物理学著作之一。书中明确指出,“光来自于眼睛所见的物体”。海桑是一位通才(阿拉伯语里叫哈基姆),除了光学,他在数学、天文学、心理学、医学等领域都有建树。他在开罗艾资哈尔大学任教授时,首次提出科学方法,他也被认为是第一个阿拉伯科学家、“科学方法论之父”。

海桑«光学»的拉丁文版封面

欧几里得证明的命题六是:

处于平行位置,大小相同距离不同的物体,在眼中看到的大小并不与远近成比例。

这等于说:

《原本》是古典数学的结晶,讲述的范围也超出几何学的范畴,如我们在第一章所言,书中包含许多基础数论的内容。例如,欧几里得算法(中国典籍称辗转相除法),算术基本定理,素数有无穷多个的证明,完美数的定义和偶完美数的充分条件,甚至在证明中使用了“任何正整数集合必有最小者”的假设(良序性)。遗憾的是,书中并没有提到任何一个数的递归序列。

在数学中,序列是指排成一列的对象或事件,每个元素不是在其他元素之前,就是在其他元素之后。序列可以是有限的,也可以是无限的。无论如何,它都是有次序的,例如,{M,A,R,Y}和{A,R,M,Y}是两个不同序列,正如Mary和army是两个不同的英文单词。值得一提的是,序列也是生物学的重要概念,所谓DNA序列是指组成某一个DNA分子的四种脱氧核苷酸(A,T,C,G)的排列次序。核苷酸是分子结构复杂的有机化合物,作为染色体存在于细胞核内,起到储藏遗传信息的作用。

而在数论领域,序列就是有编号的无穷数组或数的集合,通常用下标表示编号,如A={an},简称数列或序列,这里an表示该数列的第n项。数列可以是符合一定规则的数的集合,也可以是满足某种初始值和递归法则的数的集合。属于前者的出现较早,可以说俯拾皆是,例如:

正奇数序列{1,3,5,7,9,……}

偶数序列{0,2,-2,4,-4,……}

素数序列{2,3,5,7,11,……}

极限趋向于1的序列

{0.9,0.99,0.999,0.999,0.9999,……}

以圆周率为极限的序列

{3,3.1,3.14,3.141,3.1415,……}

由圆周率的各位数组成的序列

{3,1,4,1,5,9,2,……}

以上诸序列是自然存在的。用递归序列表示的数列姗姗来迟,至少,在公元后的第一个千年里没有出现,这与罗马人的统治和欧洲漫长的中世纪有关。众所周知,公元前212年,在叙拉古(今意大利西西里岛)沙盘上研究几何问题的阿基米德被入侵的罗马士兵刺死,这是一个标志性的历史事件,预示着希腊数学和灿烂的文化走向衰败。从那以后,罗马人开始了野蛮的统治。

而自从5世纪罗马帝国瓦解以来,欧洲又进入了漫长的“中世纪”,这个称谓是后来意大利人文主义者命名的,目的是把自己所处的时代与之区别开来,并与古希腊和古罗马遥相呼应。诗人彼得拉克则称其为“黑暗时代”,这与流行了数个世纪的黑死病不无关系。那段时间整个欧洲的数学停滞不前,数学的主要成就是由中国、印度和阿拉伯等东方国家取得的。

教皇热尔贝与魔鬼(１４６０年漫画)

大约在公元1000年前后,虽然距离中世纪结束依然十分遥远,但欧洲的数学出现了某种转机,或者说是曙光。999年4月2日,一位酷爱数学的法国学者、教师热尔贝(Gerbert,约945—1003)当上了教皇,他也是第一位法国人教皇,自称西尔维斯特二世。在任期间,热尔贝坚决反对买卖神职和用人唯亲,要求神职人员保持独身生活。据说,热尔贝能够登上教皇的宝座与他擅长数学不无关系。

热尔贝出生在法国中部的奥弗涅大区,年轻时旅居西班牙三年,曾在巴塞罗那以北60公里的一座修道院学习毕达哥拉斯学派倡导的“四艺”。伊比利亚半岛因为被阿拉伯人侵占并统治,所以具有较高的数学水平。虽说那会儿从阿拉伯语到拉丁语的后翻译时代还没有正式开始,大量的古希腊著作尚没有被译成拉丁语,热尔贝却已掌握了相当多的数学和天文知识技能。不难推测,他应该精通阿拉伯语。

969年,热尔贝陪同一位伯爵来到教廷所在地罗马,觐见教皇约翰八世和神圣罗马帝国皇帝奥托一世,他因数学才能出众受到赏识。那时候教皇由皇帝任命,而教皇主持皇帝的加冕礼。热尔贝深得奥托一世的赏识,受聘为王子、未来的奥托二世的教师。后来几任皇帝也很器重他,奥托三世任命他做了教皇(若非奥托二世早逝,他可能会更早地成为教皇)。

据说,热尔贝从阿拉伯数学家花拉子密的著作中学会了印度—阿拉伯数码,并率先把它引入西班牙以外的欧洲。他还把东方人发明的算盘介绍到欧洲,用来帮助计算。此外,他还制造出钟、管风琴和某些天文仪器。

在热尔贝撰写的一部几何学著作里,他还解决了这样一个数学问题:已知直角三角形的斜边和面积,求出它的两条直角边。这个问题在今天看来可以成为中学数学的考试题。设直角三角形的斜边长和面积分别是c和S,要求的两条直角边长分别是a和b。由三角形面积公式和勾股定理,不难知道它们满足下列二元二次方程组:

将第一个公式的4倍依次加到第二个公式两边,可得(a+b)2=c2+4S。两端开根号,即得:

同理,将第一个公式的4倍去减第二个公式,可得(a-b)2=c2-4S。两端开根号,即得:

由此不难得到:

依照12世纪一位英国教士撰写的书里的描述,热尔贝在西班牙期间,曾去文化中心科尔多瓦和塞尔维亚学习数学,有一次他偷走了一本书,被发现后把书藏在一座木桥下面躲过了搜查。1003年,在一次反对皇帝的平民叛乱期间,热尔贝死于罗马城,他的遗体下葬在今天梵蒂冈北面约四公里处的圣约翰·拉特兰教堂。可以说,热尔贝的出现是欧洲数学复兴的一丝曙光。在热尔贝身后一个多世纪,意大利诞生了历史上第一位大数学家斐波那契。

斐波那契

在数学史上,沿用至今最早的递归数列出现在13世纪初,是由意大利数学家斐波那契发现和定义的。斐波那契(Fibonacci,约1175—1250)出生于比萨,本名Filius Bonacci,意为波那契的儿子。Fibonacci这个缩写后的名字,是在1838年才由意大利人利伯里(1) (Libri, 1803—1869)给取的。利伯里是一位伯爵和数学爱好家,因其对古代珍贵手稿的热爱和窃书而闻名。

斐波那契塑像(1863,比萨营地)

不仅如此,斐波那契数列与毕达哥拉斯学派的黄金分割比也有着密切关系。简而言之,前一项与后一项的比值在项数趋向无穷时的极限为黄金分割比。这个序列除了在数论和许多其他数学分支中常常见到以外,在现代物理、准晶体结构和股票分析等领域都有直接的应用,还可以帮助解决诸如蜜蜂的繁殖、雏菊的花瓣排列、艺术美感和设计诸方面的问题。

斐波那契家境富裕,他的父亲是比萨共和国的政府官员,曾被派往布日伊(Bougie,今属阿尔及利亚)任商务代理。斐波那契童年时便跟随父亲到了北非,在那里学会了印度—阿拉伯数码。后来,他又随父亲到过埃及、叙利亚、拜占庭(希腊)、西西里和普罗旺斯等地,通过广泛深入的学习和研究,他掌握了数学尤其是计算方面的各种技巧。

12世纪末,斐波那契回到比萨,在那里度过了四分之一世纪。他在故乡著书立说,并在书中采用印度—阿拉伯数码书写,促进了这一数码体系在欧洲的普及。记数和计算则利用巴比伦人发明的60进制,同时他也把数学应用于商业活动的各个领域。斐波那契还阐述了许多代数和几何问题,其重要成果主要表现在不定分析和数论领域,远远超越了前人。(www.xing528.com)

大约在1225年,斐波那契受到神圣罗马帝国皇帝腓特烈二世的召见,成为宫廷数学家。据说皇帝的随从向他提出数学问题,他都一一解答。这位皇帝喜欢打仗、美女,也热爱诗歌和数学,他是欧洲好多位名号为腓特烈二世的君主之一,虽说不是最有名的一个,但他却拥有多个国王头衔,按时间顺序分别为西西里国王(1197)、德意志国王(1212)、神圣罗马帝国皇帝(1220)和耶路撒冷国王(1229)。

腓特烈二世的宫殿自然也有许多处,个人猜测斐波那契是待在西西里王国,那是腓特烈二世度过童年的地方。虽说这位国王有着包括日耳曼等多个民族的血统,但他并不真正喜欢德意志。1224年,腓特烈二世在西西里王国的都城那不勒斯创建了欧洲第一所国立大学(1978年该校以腓特烈二世冠名),其最杰出的毕业生是哲学家托马斯·阿奎那(Thomas Aquinas,约1225—1274)。事实上,那时在南部意大利,那不勒斯王国与西西里王国是合二为一的。

说到那位天主教世界最重要的哲学家托马斯·阿奎那,他比斐波那契要年轻一辈。1225年,当斐波那契被国王腓特烈二世召见时,他出生在那不勒斯的洛卡塞卡城堡,那是他家族的领地。16岁那年,他进入那不勒斯大学,后来在巴黎大学获得神学博士学位。阿奎那的代表作是《神学大全》,该书翔实地讨论了天主教的所有教义。此外,他还给出了上帝存在的五个证明。托马斯·阿奎那把理性引入神学,同时宣称:“没有一种智慧可以不经由感觉而获得。”

至于斐波那契是否曾在那不勒斯逗留,我们就不得而知了。由于腓特烈二世忙于征战,以及与控制欲极强的教皇之间的重重矛盾,斐波那契不大可能在这位国王的宫殿里停留太久。事实上,1240年,在他的故乡比萨留存下来的一份文件上这样写道:由于斐波那契曾向市民和官吏讲述计算方法,每年给予他薪水若干金币。换句话说,他有可能在故乡度过晚年并在那里去世。

斐波那契共有五部著作传世,包括《花》《平方数书》《算盘书》《实用几何》和《给帝国哲学家狄奥多鲁斯的一封未注明日期的信》。《花》是题献给腓特烈二世的,书中收入了宫廷里举行的数学竞赛问题。例如,二次方程x2±5=y2的解。他还证明了,三次方程:

既没有整数或有理数解,也没有欧几里得的无理量解,即用直尺和圆规作出的根。但他却得到一个小数点后11位数的近似解,即x=1.36880810785,无人知道他是如何得到这个结果的。

值得一提的是,由于那个时代的欧洲代数尚未符号化,斐波那契是用几何的语言来叙述的。例如,《平方数书》里有讲到方程4x-x2=3,他是这样表述的:

如果从正方形的四条边减去它的面积,则得3竿。

当然,斐波那契最著名的著作要数《算盘书》(1202)。此处算盘是指用以计算的沙盘,而非真的算盘。书中引进了分数中间的那条横杠“—”,这是迄今我们仍在使用的符号。还有类似于“百鸡问题”的不定方程,那应是受到中国古代数学的影响,这种影响可能是通过阿拉伯人的著作传递的。此外,他还讲述了求方根的方法和比例变换。不过,最有趣最重要的还是要数“兔子问题”。

神性的兔子

所谓“百鸡问题”出现在中国南北朝时期,北魏数学家张丘建(又作张邱建)的著作《张丘建算经》中记载了这一问题。该书大约成书于公元466—485年,幸运地流传至今。其时北魏首都在平城(山西大同),统治者是鲜卑族人。日本古都、6—8世纪的文化艺术中心平城京(奈良)虽是仿长安而建,但其取名应与平城有关。

张丘建的家乡在清河县(今属河北邢台市),其算经中最后一道题堪称亮点,通常被称为“百鸡问题”,民间流传着县令以此考问神童的佳话。原文如下:

今有鸡翁一,直钱五;鸡母一,直钱三;鸡雏三,直钱一。凡百钱买鸡百只,问鸡翁、母、雏各几何?

意思是,公鸡每只五钱,母鸡每只三钱,而雏鸡三只才一钱。假设有一百钱,去买一百只鸡(钱必须用光),问需买多少只公鸡、母鸡和雏鸡?

设欲购买的公鸡、母鸡和雏鸡的数量分别是x、y、z,此题相当于解下列方程组的正整数解:

在张丘建时代,中国尚未引进字母,也没有未知数的概念,用文字叙述这样的方程组必定是很不容易的。可是,张丘建却正确地给出了全部三组解答,即(4,18,78),(8,11,81)和(12,4,84)。实际上,他通过消元法,把这两个三元一次方程化成一个二元一次方程,即:

7x+4y=100

再依次取x为4的倍数,即得上述三组解答。

而所谓“兔子问题”是这样的:由一对小兔开始,一年后可以繁殖成多少对兔子?其中规定:每对大兔每月能生产一对小兔,而每对小兔两个月后就成为可以繁殖的大兔。依据“兔子问题”,很容易得到所谓的斐波那契数或斐波那契数列,其前十项是:

1,1,2,3,5,8,13,21,34,55……

这个序列的递归公式(数学家发现和定义的第一个递归公式)是:

有意思的是,这个数列的通项竟然含有无理数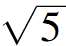。而前一项与后一项的比值依次是:

1,0.5,0.666…,0.6,0.625,0.615…,0.619…,0.617…,0.618…

没错,这个数列存在极限,且这个极限值恰好就是美学中非常重要的黄金分割比。只是,直到四个世纪以后的1611年,这个极限值才由德国天文学家、数学家开普勒(Johannes Kepler,1571—1630)发现,他猜测这个极限就是古希腊的毕达哥拉斯学派定义的黄金分割比,即

至于这个极限值的证明,至晚在19世纪,才由法国数学家比奈(Jacqttes Binet,1786—1856)给出。

边长为斐波那契数的正方形折叠

在笔者所著《数之书》及《经典数论的现代导引》中、英文版中,序言的插图均严格依照斐波那契数排列,即第1页2幅插图,第2、3、5、8和13页各有1幅插图。在自然界中,斐波那契数列也有意想不到的呈现。以植物界为例,许多花朵的花瓣个数恰好是斐波那契数,例如,梅花5瓣、飞燕草8瓣、万寿菊13瓣、紫苑21瓣,而雏菊34瓣、55瓣或89瓣的都有。

另外,有一个很有趣的爬楼梯的例子。假设你可以一步登一个台阶,也可以一步登两个台阶。试问,攀登一个有n个台阶的楼梯有多少种方式?

设共有an种方式,易知a1=1,a2=2。进一步分析:假设第一步登了一个台阶,则还有an-1种选择;而假设第一步登了两个台阶,则还有an-2种选择。这样一来,就得到:

比较上式和斐波那契数列的定义及其初始值,即可得an=Fn+1。

斐波那契数列有许多有趣的性质,它还有一些未解之谜。例如,是否有无穷多个斐波那契数是素数?

1680年,巴黎天文台台长卡西尼(Giovanni Cassini,1625—1712)发现了下列恒等式:

后来它被称作卡西尼恒等式。1879年,比利时出生的法国数学家卡塔兰(Eugène Catalan,1814—1894)将卡西尼恒等式推广为(卡塔兰恒等式):

当r=1时,此即为卡西尼恒等式。正是卡塔兰,命名了斐波那契数列。

从斐波那契留下来的画像来看,他的神韵颇似晚他三个世纪的同胞画家拉斐尔。斐波那契常常以旅行者自居,人们喜欢称他是“比萨的莱奥拉多”,而把《蒙娜丽莎》的作者称为“芬奇的莱奥拉多”。我们可以这么说,斐波那契既是欧洲数学复兴的先锋,也是东西方数学交流的桥梁。

斐波那契肖像

1963年,世界各国一群热衷研究“兔子问题”的数学家成立了国际性的斐波那契协会,并着手在美国出版《斐波那契季刊》(Fibonacci Quarterly),专门刊登研究与斐波那契数列有关的数学论文。同时,又两年一度在世界各地轮流举办斐波那契数列及其应用国际会议。这在世界数学史上,也可谓是一个奇迹或神话了,堪称神性的兔子。

相比之下,“百鸡问题”只是一个孤立的初等数论问题,没有可持续研究的内容。不过,比斐波那契晚20多年出生的中国南宋数学家秦九韶(1202—1261)却将4世纪《孙子算经》里的“物不知数”问题加以拓广,推导出了中国剩余定理。至今这个定理仍在许多数学领域有着广泛的应用,被东西方每一本初等数论教科书收录,而按照国际惯例,它应该被称为秦九韶定理。