一、选择题:1-8小题,每小题4分,共32分.每小题给出的四个选项中,只有一个选项是符合题曰要求的,请将选项前的字母填写在答题纸指定位置上.
(1)设函数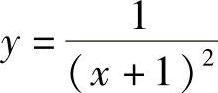 ,则y(n)为
,则y(n)为
[ ]
(2)设二元函数f(x,y)在点(x0,y0)处的三个2阶偏导数f″xx(x,y),f″xy(x,y),f″yx(x,y)存在,则必有
(A)f″xy(x0,y0)=f″yx(x0,y0). (B)fx′(x,y)在点(x0,y0)处可微.
(C)fx′(x,y)在点(x0,y0)处连续. (D)fx′(x,y0)在点x0处可微.
[ ]
(3)级数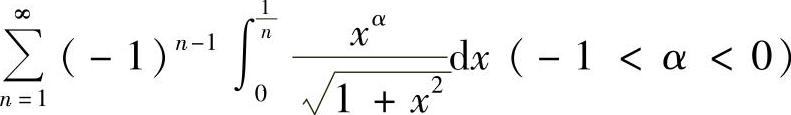
(A)绝对收敛. (B)条件收敛.
(C)发散. (D)收敛或发散与α取值有关.
[ ]
(4)设y1,y2是非齐次线性微分方程y′+p(x)y=q(x)的两个特解,若常数λ,μ使λy1+μy2是该方程的解,λy1-μy2是该方程对应的齐次方程的解,则
[ ]
(5)设矩阵方程AX=B(其中A是m×n矩阵,B是m×l矩阵,X是n×l未知矩阵),则该方程有无穷多解的充分必要条件为
(A)r(A︙B)=r(A)=n. (B)r(A︙B)=r(A)<n.
(C)r(A︙B)>r(A). (D)r(A︙B)=r(A).
[ ]
(6)设A,B都是n阶实对称矩阵,则A与B合同的充分必要条件为
(A)r(A)=r(B).
(B)|A|=|B|.
(C)A,B的特征值相同.
(D)分别以A,B为矩阵的二次型有相同的规范形.
[ ]
(7)设X,Y是随机变量,其中X~N(1,1),概率密度为f1(x),Y的概率密度为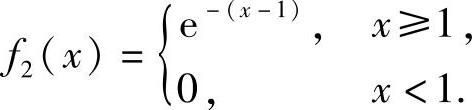 记
记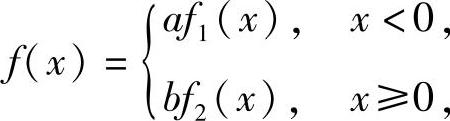 则当f(x)是概率密度时,a,b应满足
则当f(x)是概率密度时,a,b应满足
[ ]
(8)设X1,X2,…,Xn是来自总体X的简单随机样本,其中X服从参数λ的指数分布.记样本均值为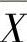 ,方差为S2,则当
,方差为S2,则当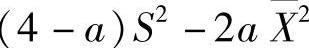 为
为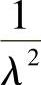 的无偏估计量时,常数a为
的无偏估计量时,常数a为
(A)3. (B)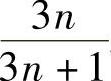 . (C)
. (C)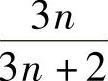 . (D)
. (D)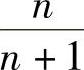 .
.
[ ]
二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9)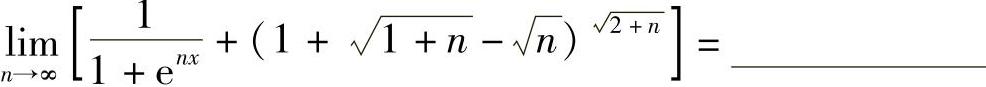 .
.
(10)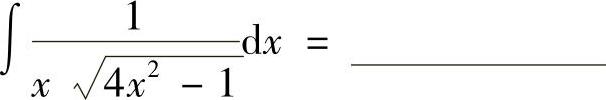 .
.
(11)设二元函数f(u,v)可微,则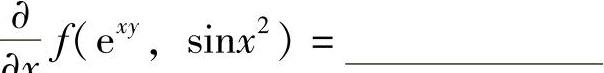 .
.
(12)幂级数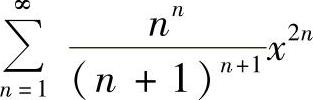 的收敛域为____.(https://www.xing528.com)
的收敛域为____.(https://www.xing528.com)
(13)设矩阵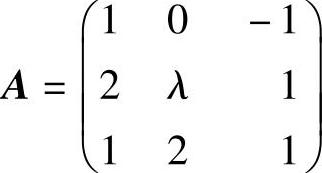 及3阶矩阵B,它们满足r(B)=2,r(AB)=1,则λ=____.
及3阶矩阵B,它们满足r(B)=2,r(AB)=1,则λ=____.
(14)设A,B,C是相互独立事件,且P(A)=0.4,P(B)=P(C)=0.5,则概率P(A-C|AB∪C)=____.
三、解答题:15-23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
设函数y=φ(ψ(x)),其中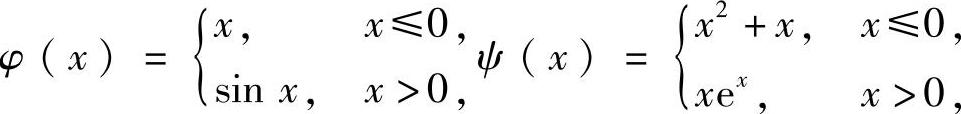 求φ′(ψ(x))x=0与[φ(ψ(x))]′x=0.
求φ′(ψ(x))x=0与[φ(ψ(x))]′x=0.
(16)(本题满分10分)
已知二元连续函数f(x,y)满足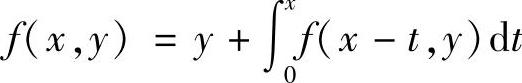 ,求二重积分∬
,求二重积分∬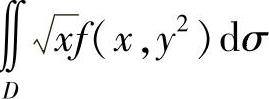 ,其中D是由曲线x=y2和直线x=1围成的区域.
,其中D是由曲线x=y2和直线x=1围成的区域.
(17)(本题满分10分)
某厂家生产的一种产品同时在A,B两个市场销售,每件产品售价分别为p1和p2,需求函数分别为q1=3-0.5p1和q2=2-3p2,总成本函数为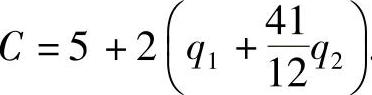 .如果A市场的价格对B市场的价格弹性为2,且p2=1时,
.如果A市场的价格对B市场的价格弹性为2,且p2=1时,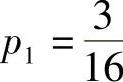 .试问:厂家如何确定两个市场的售价,能使其获得的总利润最大?
.试问:厂家如何确定两个市场的售价,能使其获得的总利润最大?
(18)(本题满分10分)
设f(x)是[0,1]上非负、单调减少的连续函数,证明:
(19)(本题满分10分)设幂级数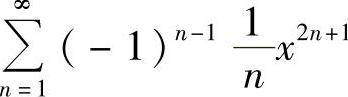 ,求
,求
(Ⅰ)该幂级数的和函数s(x)及其定义域;
(Ⅱ)方程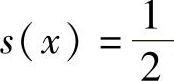 的实根个数.
的实根个数.
(20)(本题满分11分)
设A是三阶矩阵,α1,α2,α3是线性无关的三维列向量组.已知
Aα1=α2+α3,
Aα2=α1+aα3,
Aα3=α1+α2,
问:a为何值时,A不能相似对角化?
(21)(本题满分11分)
设二次型f(x1,x2,x3)=xTAx(其中x=(x1,x2,x3)T,A是3阶实对称矩阵)经正交变换x=Qy(其中y=(y1,y2,y3)T,Q是正交矩阵)化为标准形2y21-y22-y23.又设A∗α=α(其中A∗是A的伴随矩阵,α=(1,1,-1)T).求
(Ⅰ)Q及A;
(Ⅱ)可逆线性变换x=Cz(其中z=(z1,z2,z3)T,C是可逆矩阵),它将f(x1,x2,x3)化为规范形.
(22)(本题满分11分)
设随机变量X是连续型的,它的概率密度为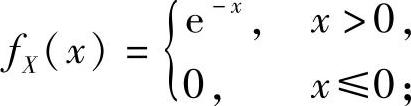 随机变量Y是离散型的,它的概率分布为
随机变量Y是离散型的,它的概率分布为
(Ⅰ)当X与Y相互独立时,求Z=XY的分布函数FZ(z);
(Ⅱ)求Cov(X,X2).
(23)(本题满分11分)
设X1,X2,…,Xn是来自总体X~N(0,1)的简单随机样本,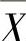 ,S2分别是它的均值与方差,求
,S2分别是它的均值与方差,求
(Ⅰ)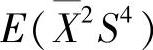 ;
;
(Ⅱ)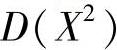 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




