本节介绍决策信息系统属性增加后基于矩阵方法的动态属性约简更新原理和算法.
4.1.1.1 属性增加时基于知识粒度和矩阵方法的动态属性约简原理
当在决策信息系统中添加属性集P 时，可能引起决策信息系统的等价类被细化，从而导致决策信息系统的知识粒度变小，换句话说，原来等价关系矩阵的元素mij可能从1 变为0.定义4.1 和4.2 分别介绍了属性增加时基于矩阵方法的计算决策信息系统知识粒度的增量机制.
定义 4.1 已知决策信息系统S＝（U，A＝C∪D，V，f），
假设P 是增量属性集，RP是论域U 上的一个等价关系，
增加属性后的增量等价关系矩阵
的元素定义为：
下面通过一个例子来说明定义4.1 中计算增量等价关系矩阵的过程.
例4.1（续例2.1）假设P＝{g，h}是增量属性集，见表4-1.
表4-1 增量属性集
根据定义2.14 可得：
根据定义4.1，增量等价关系矩阵为：
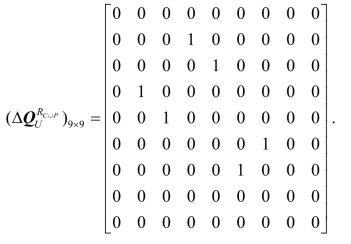
定义4.2 已知决策信息系统S＝（U，A＝C∪D，V，f），
假设P 是增量属性集，RP是论域U 上的一个等价关系，
则增加属性后的增量等价关系矩阵
的元素定义为：
定理4.1 已知决策信息系统S＝（U，A＝C∪D，V，f）是一个决策信息系统，假设决策信息系统条件属性的知识粒度是GPU（C）.P 是增量属性集，
是增量等价关系矩阵.增加属性集后决策信息系统的知识粒度为：
证明 由定义易得定理成立.
定理4.2 已知决策信息系统S＝（U，A＝C∪D，V，f），假设决策信息系统条件属性和决策属性的知识粒度为GPU（C∪P）.P 是增量属性集，
是增量等价关系矩阵.决策信息系统添加属性集P 后条件属性和决策属性的知识粒度为：(www.xing528.com)
证明 由定义易得定理成立.
定理4.3 已知决策信息系统S＝（U，A＝C∪D，V，f），
和
是决策信息系统的等价关系矩阵，假设决策信息系统决策属性D 关于条件属性C 的知识粒度是 GPU（D|C）.P 是增量属性集，
和
是增量等价关系矩阵.决策信息系统增加属性后决策属性D 关于条件属性C∪P的相对知识粒度为：
证明 由定义2.16 可得：
因为：
所以：
例4.2（续例4.1） 根据定义4.2 可得：
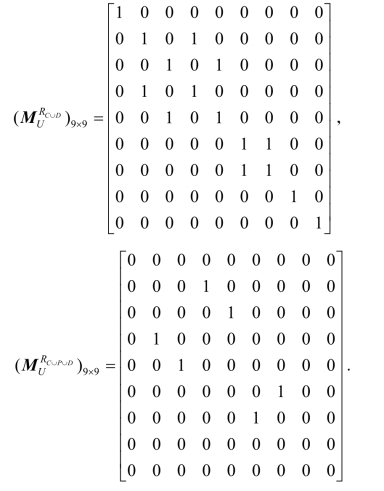
因为GPU（D|C）＝
，故：
4.1.1.2 属性增加时基于知识粒度和矩阵方法的动态属性约简算法
当在决策信息系统中添加属性时，非动态属性约简算法需要重新计算变化后决策信息系统的知识粒度和属性约简，导致计算时间耗费巨大.为了提高效率，我们设计了基于矩阵方法的动态属性约简算法.该方法在原来决策信息系统知识粒度和属性约简的基础上，能够快速获得决策信息系统变化后的属性约简.基于知识粒度和矩阵方法的动态属性约简算法如算法4.1 所述，基于知识粒度和矩阵方法的动态属性约简算法框架图如图4-1 所示.
图4-1 增加属性后的动态属性约简算法框架图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
