本节利用UCI 机器学习数据集进行了大量实验以验证所提出的基于非矩阵方法的动态属性约简算法的高效性.实验仿真方案与实验性能分析过程介绍如下.
3.1.5.1 实验方案
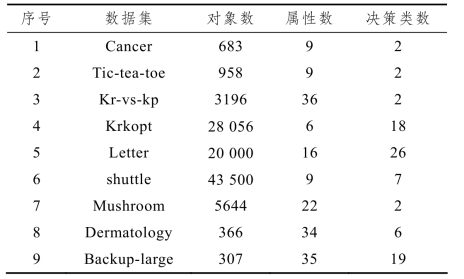
我们从UCI 机器学习公用数据集上下载了9 个数据集进行实验.下载的9 个数据集的具体描述如表3-3 所示.我们用Microsoft C#来编写所提出的算法.实验过程中所用的计算机硬件和软件配置环境为:CPU:Inter Core2 Quad Q8200,2.66 GHz,内存:4.0 GB;操作系统:64-bit Windows 7.另外,本章所提出的基于矩阵、非矩阵方法的动态属性约简算法主要以完备决策信息系统为研究对象,因此,对于不完备决策信息系统中具有缺失的数据,在实验过程中进行简单删除即可.在实验过程中,由于计算机运行时间不稳定,为了让运行时间更具有代表性,我们把多次运行的时间取平均值作为属性约简的计算时间,本章取10 次运行时间的平均值作为实验最终结果值.
表3-3 数据集的具体描述
我们通过以下几组实验来验证所提出算法的有效性:
(1)针对不同数据集,对对象变化(增加或删除)时动态属性约简算法和非动态属性约简算法的运行结果进行比较,具体实验方案如下:
在实验中,把表3-3 数据集中的对象均匀分成两部分,第一部分数据集是基本数据集,第二部分数据集作为增量数据集(或者成为被删除数据集),当增量数据集添加到基本数据集(或者从整个数据集中删除该数据集)时,分别用动态属性约简算法和非动态属性约简算法来运行每个数据集.
(2)针对同一数据集中不同大小对象集,对对象变化(增加或删除)时动态属性约简算法和非动态属性约简算法的运行结果进行比较,具体实验方案如下:
在实验中,首先把表3-3 数据集中的对象均匀分成两部分,把其中一部分数据集作为基本数据集,另外一部分数据集中的对象再均匀分成5 部分并依次作为增量数据集(或者成为被删除数据集),当增量数据集依次添加到决策信息系统(或者依次从决策信息系统删除该数据集)时,分别用动态属性约简算法和非动态属性约简算法来运行每个数据集.
(3)针对不同数据集,对对象变化(增加或删除)时动态属性约简算法和非动态属性约简算法的近似分类精度和近似分类质量进行比较,具体实验方案如下:
在实验中,运用粗糙集中近似分类精度和近似分类质量两个评价指标分别对动态属性约简算法和非动态属性约简算法所获得的属性约简的有效性进行分析,当所找到的属性约简的近似分类质量和近似分类精度的值相等或相近时,说明所找到的属性约简是有效的.
(4)针对不同数据集,对对象变化(增加或删除)时动态属性约简算法和非动态属性约简算法的分类精确度结果进行比较,具体实验方案如下:
在实验中,运用十字交叉方法分别对动态属性约简算法和非动态属性约简算法所计算的属性约简的分类精确度进行比较,即把表3-3 数据集中的对象分成90%和10%两部分,其中90%的部分数据集在实验过程中作为训练集,剩余10%的部分数据集在实验过程中作为测试集,利用贝叶斯分类方法运行每个数据集.
(5)针对不同数据集,对对象增加时所提出的基于非矩阵方法的动态属性约简算法和其他动态属性约简算法的实验结果进行比较,具体实验方案如下:
在实验中,把表3-3 数据集中的对象均匀分成两部分,把其中一部分数据集作为基本数据集,另外一部分数据集作为增量数据集,当增量数据集被添加到基本数据集时,分别用基于非矩阵方法的动态属性约简算法和基于信息熵的动态属性约简算法运行每个数据集.
3.1.5.2 性能分析
以上各实验结果分别介绍如下:
(1)决策信息系统中对象发生变化时(增加或删除),动态属性约简算法和非动态属性约简算法的运行结果比较.
当决策信息系统中对象发生变化时(增加或删除),分别用非动态属性约简算法、基于矩阵、非矩阵方法的动态属性约简算法来更新决策信息系统的属性约简,实验结果比较如表3-4 和表3-5 所示.由于算法MIARC、IARC 计算的属性约简数目、属性约简数值是一样的,所以在表3-4 中对算法IARC 仅列出计算时间.实验结果表明:非动态属性约简算法、基于矩阵、非矩阵方法的动态属性约简算法所得到的属性约简数目(NFS)、属性约简数值是相近的,甚至有些数据集的属性约简是相等的,但是对于决策信息系统对象增加时,基于矩阵方法的动态属性约简算法的运行时间小于非动态属性约简算法的更新时间,基于非矩阵方法的动态属性约简算法的更新时间小于基于矩阵方法的动态属性约简算法的更新时间;针对一些对象从决策信息系统被删除,从表3-5 可看出,动态属性约简算法的时间远远小于非动态属性约简算法的运行时间.因此,动态属性约简算法在实际中具有较好的适应性.
表3-4 比较算法CAR、MIARC 和IARC 的运行结果

表3-5 比较算法CAR 和UARD 的运行结果

(2)不同大小对象增加或删除时,动态属性约简算法和非动态属性约简算法的运行结果比较.
当不同大小对象发生变化时(增加或删除),分别用非动态属性约简算法、基于矩阵、非矩阵方法的动态属性约简算法来更新决策信息系统的属性约简,实验结果比较如表3-6、表3-7 和表3-8 所示.分别把大小不同的对象添加到基本数据集(或者从决策信息系统删除对象)并进行测试,仿真实验结果比较如图3-2、图3-3 及图3-4 中的每个子图所示.图中X 轴为增加大小不同的对象,Y 轴为更新属性约简的运行时间,单位为秒(s).图中圆圈线表示增量更新属性约简的运行时间,方格线表示非动态属性约简算法的运行时间.实验结果表明:动态属性约简算法和非动态属性约简算法所得到的属性约简数目、属性约简数值是非常相近甚至有些数据集的属性约简是相等的,但动态属性约简算法的计算时间远远小于非动态属性约简算法的计算时间.另外,图3-2、图3-3 和图3-4 显示:随着决策信息系统对象发生变化时(增加或删除),基于矩阵、非矩阵方法的动态属性约简算法和非动态属性约简算法的更新时间都有所增加,但非动态属性约简算法的更新时间增加得更多.结果验证了动态属性约简算法更适合处理动态变化数据集.
表3-6 比较算法CAR 和MIARC 的运行时间(s)(https://www.xing528.com)

表3-7 比较算法CAR 和IARC 的运行时间(s)

表3-8 比较算法CAR 和UARD 的运行时间(s)
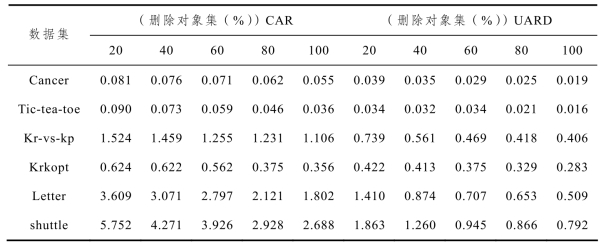


图3-2 对象增加时基于矩阵方法的动态属性约简运行时间与 非动态属性约简运行时间比较
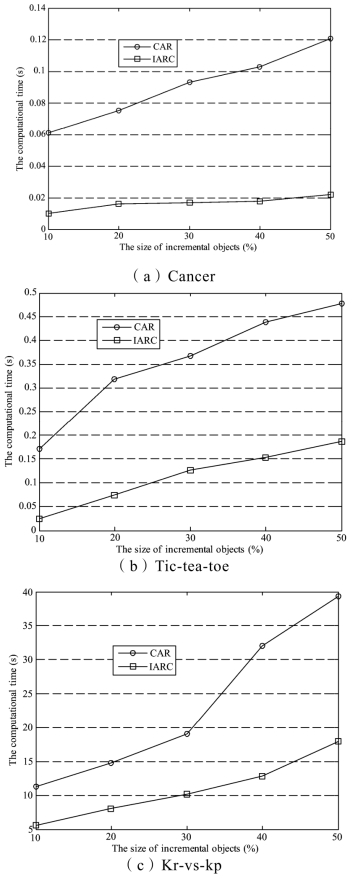
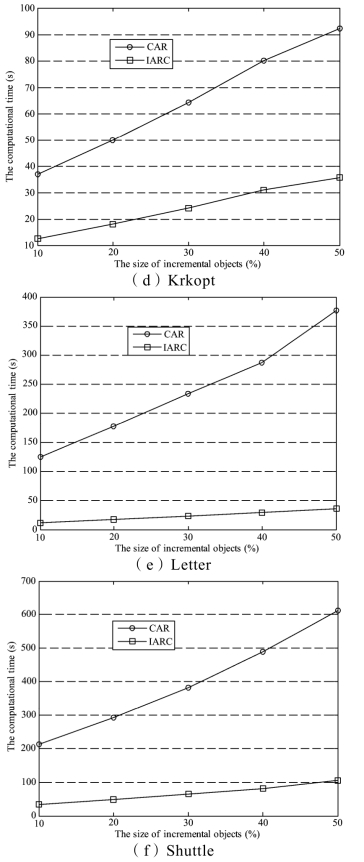
图3-3 对象增加时基于非矩阵方法的动态属性约简运行时间与 非动态属性约简运行时间比较


图3-4 对象删除时基于非矩阵方法的动态属性约简运行时间与 非动态属性约简运行时间比较
(3)对象增加或删除时,动态属性约简算法和非动态属性约简算法所计算的属性约简的近似分类精度和近似分类质量结果比较.
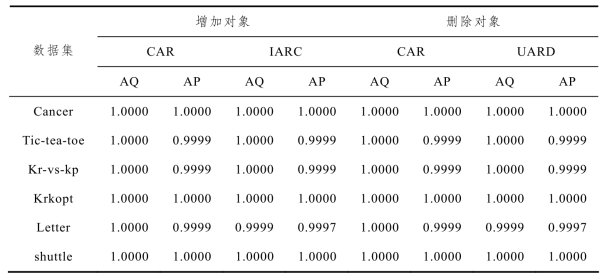
当一些对象增加到决策信息系统或从决策信息系统被删除时,运用粗糙集中近似分类精度和近似分类质量两个评价指标分别对动态属性约简算法和非动态属性约简算法所获得的属性约简的有效性进行分析,结果比较如表3-9 所示.结果表明:动态属性约简算法和非动态属性约简算法所计算的属性约简的近似分类精度和近似分类质量数值是非常相近甚至有些数据集的近似分类精度和近似分类质量是相等的.结果验证了动态属性约简算法所得到的属性约简是有效的.
表3-9 比较算法CAR、IARC 和UARD 的近似分类精度和近似分类质量
(4)对象增加或删除时,动态属性约简算法和非动态属性约简算法所计算的属性约简的分类精确度结果比较.
当对象增加或删除时,运用十字交叉方法分别对动态属性约简算法和非动态属性约简算法所得到的属性约简的分类精确度进行分析比较,用贝叶斯分类方法运行每个数据集的结果如表3-10 所示.结果表明:动态属性约简算法和非动态属性约简算法所计算的属性约简的分类精确度在大部分数据集上的结果是相等的甚至在个别数据集的分类精确度有所提高.结果表明:动态属性约简算法能够有效处理决策信息系统中对象变化的数据集.
表3-10 比较算法CAR、IARC 和UARD 的分类精确度(%)

(5)对象增加时基于非矩阵方法的动态属性约简算法与其他动态属性约简算法实验结果比较.
当一些对象增加到决策信息系统中时,分别用基于非矩阵方法的动态属性约简算法和基于信息熵的动态属性约简算法运行每个数据集,结果比较如表3-11 所示.结果表明:基于非矩阵方法的动态属性约简算法和基于信息熵的动态属性约简算法所得到的属性约简数目、属性约简是非常相近甚至有些数据集的属性约简是相等的,但是算法IARC 的计算时间小于算法 GIARC 的计算时间.实验仿真结果验证了所提出的算法IARC 能够有效处理动态变化决策信息系统.
3-11 比较知识粒度动态属性约简算法和信息熵动态属性约简算法运行结果

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




