经典粗糙集模型的研究成果

本节简要介绍经典粗糙集模型的相关知识及基本概念[6，148].

定义2.1[148]决策信息系统S＝（U，A＝C∪D，V，f）是四元组，其中U为非空有限对象集合，称为论域；A＝C∪D是非空有限属性集合，C和D分别是条件属性集和决策属性集；为决策信息系统属性集的值域，其中属性a 的值域为 Va；决策信息系统的信息函数 f ：U×（C∪D）→V，且a∊C∪D，x∊U，有 f（x，a）∊ Va.

定义2.2[148]S＝（U，A＝C∪D，V，f）是决策信息系统，∀P⊆C，论域U 的不可分辨关系定义为：

显然，不可分辨关系是一个等价关系.它产生论域U 的划分为 U/RP，U/RP＝{E1，E2，…，Em}是由等价关系 RP 形成的等价类集合.由等价关系 RP形成的等价类＝{y|（x，y）∊RP}是粗糙集理论中的基本知识粒.

在粗糙集理论中引入上近似集和下近似集以便对U 中任意子集进行近似描述，定义如下：

定义　2.3[148]已知决策信息系统S＝（U，A＝C∪D，V，f），R 是一个等价关系，∀X⊆U，X 关于R 的下近似集和上近似集分别定义为：

论域U 被X 的上、下近似集划分为正区域POSR（X）、负域NEGR（X）及边界域BNDR（X）三个不相交的区域.

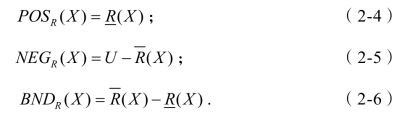
下面通过一个实例来解释上述的基本定义.(www.xing528.com)

例2.1 表2-1 是一个决策信息系统，其中论域U＝{1，2，3，4，5，6，7，8，9}，条件属性集C＝{a，b，c，f，e}，决策属性集D＝{d}.

表2-1　一个决策信息系统

从表2-1 得：

U＝{xi|1≤i ≤ 9}，C＝{a,b,c,f,e}，D＝{d}；

Va＝{0,1}，Vb＝{0,1}，Vc＝{0,1}，Vf＝{0,1}，Ve＝{0,1}，Vd＝{0,1}；

U/C＝{E1,E2,E3,E4,E5}，

其中，E1＝{1}，E2＝{2，4}，E3＝{3，5}，E4＝{6，7}，E5＝{8，9}.假设X＝{1，2，3，6，7}，则：