1.无符号整数的编码
假设用4bit(四个二进制的位)来表示整数。二进制只有两个符号“0”和“1”,每一个二进制的位或者为“0”或者为“1”。长度为4的二进制位串共有16(24)个,见表0-2的第一列。按与十进制计数体系类似的方式来理解,如十进制的1024,可展开为多项式:1024 = 1×103 + 0×102 + 2×101 + 4×100。
表0-2 无符号整数的编码

续表

采用这种方式编码,没有包含负整数,即这只是“无符号整数”编码。其表示的整数范围是0~15。依此类推,目前32位的机器采用32bit来表示整数,如何用来表示无符号整数,能表示的范围是多少?在C语言中,用关键字unsigned int声明无符号整数,而用int表示有符号整数。
2.有符号整数的编码
对有符号数,需要用一个二进制位表示符号位,如果取最高位(最左边的位)作符号位,并且人为规定最高为位为0表示正数,为1表示负数。那么,最直观的编码方式是,用剩下的位表示整数的绝对值大小。则位串“1111”表示-7,而0会有两种编码表示“0000”和“1000”,因此,计算机采用另外一种编码来表示有符号整数,即“二进制补码”。
先通过一个例子来解释补码的原理:比如我们熟悉的时钟,共12个刻度。如果按无符号整数来理解,每个刻度分别对应于0点、1点、2点……11点。如果按有符号整数来理解,将11点钟方向理解成-1点,并依此类推,这是一个有符号的时钟,见图0-3。

图0-3 有符号的时钟
也许有人会问:为什么不能把6点钟方向标为“-1”,而要把11点钟方向标为“-1”呢?原因是这样编码,更适合计算机进行数据的运算,可以将减法运算用加法的方式来处理。以这个时钟为例,“加法”相当于顺时针拨动指针,“减法”对应于逆时针拨动指针,采用这种“补码”编码方式,就可以只保留“加法”操作。即逆时钟移动1个刻度,可以用顺时针移动11个刻度来实现。如:
2-1 = 2 + 11 = 13(正好对应于1)
以这个直观的例子为基础,再来解释计算机如何存储有符号整数。
先介绍两种运算:反码运算和补码运算。反码运算表示按位取反。而补码运算:从低位复制位,直到有1被复制;然后,反转其余的位。
例如:计算整数01101010的反码和补码
原来的位串 0 1 1 0 1 0 1 0
反码运算的结果 1 0 0 1 0 1 0 1
很显然,对一个位串进行两次反码运算,可以得到原来的数。
 (https://www.xing528.com)
(https://www.xing528.com)
同样,对一个位串进行两次补码运算,也可以得到原来的数。
计算机存储有符号的整数,遵循如下步骤:
● 先将整数的值变成二进制数。
● 如果是正数,原样存储;如果是负数,计算补码并存储。例如:整数-1,用补码方式存储在8位的存储单元

从二进制补码格式还原整数,计算机遵循的步骤如下:
● 最高位为1,计算机取其补码;最高位为0,不进行操作。
● 将该二进制数转换为十进制数。
例如,已知机器内的二进制位串为:10010110,最高位为“1”,它是一个负数,求补得到01101001为数值的大小,因此,该补码表示的是十进制数-105。
下面看看,在二进制补码表示整数的基础上,减法运算是如何转换成加法运算的。两个整数A、B,都用二进制补码表示,则A减B和A加B的补码得到的结果是一样的。例如:

再来看看补码10100000表示哪个整数,如果表示-95,那这个计算结果就是正确的。按前面所说的规则,最高位为1,表示是一个负数,求码得到该负数的大小:
10100000 求补运算→ 01011111 (64+16+8+4+2+1=95)
请自己分析一下10-(-105)的计算过程。
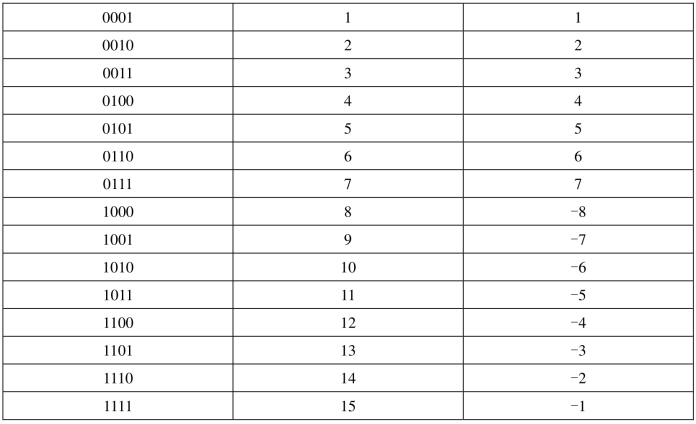
计算机看到一个二进制的位串,必须了解其确切类型,才能对它做正确的解析和进一步的操作。表0-3就是整数在计算机内的表示。自己分析一下,在32位的机器里,用32位来表示有符号整数和无符号整数,表示的数据范围是什么?
表0-3 整数的编码

![]()
续表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




