智能优化算法在Lorenz混沌系统在线参数辨识中的应用

1.算法参数设置

所有算法的迭代次数设为1000次，运行次数设为30次，变量范围a∈［5，15］，b∈［0，3］，c∈［10，40］。

BFO算法设置：与第8.3.1节中的设置相同。

PSO算法设置：粒子数为30，惯性权重w从0.9线性较小到0.5，学习因子c1=c2=2，vmax=［5，15，1.5］。

GA算法设置：与第8.3.1节中的设置相同。

2.数值仿真及结果分析

表8.3列出了三种算法对有噪声的Lorenz系统进行在线参数辨识的结果。从表8.3中可以看出BFO算法得到的最优解的精度比PSO算法和GA算法都要高，基本上已经接近实际参数值。通过标准差可以看出BFO的偏差最小，说明BFO算法的稳定性也好于PSO算法和GA算法。图8.8给出了三种算法30次独立运行在线辨识结果和相应的实际值之间的误差，可以看出基于BFO算法在线辨识得到的三个参数的误差绝大多数情况下都是最小的，进一步说明BFO算法的稳定性更优于其他算法。图8.9给出了BFO算法分别在无噪声、有噪声但不在线参数辨识和有噪声且在线参数辨识三种情形下的系统误差对比图，可以看出在叠加噪声的情形下，基于BFO算法的在线估计方法可以有效降低误差。将表8.3与表8.1相比较，可以看出即使存在噪声BFO算法在线辨识Lorenz系统的最优值精度比无噪声情形下还要好，这说明在线辨识方法可以显著提高Lorenz系统参数的辨识精度。(www.xing528.com)

表8.3　存在噪声时三种算法在线辨识Lorenz系统的结果

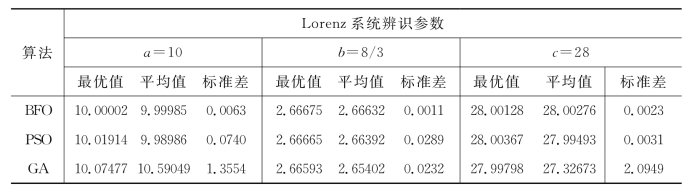
图8.8　存在噪声时，在线辨识Lorenz系统参数与实际值的误差

图8.9　BFO算法分别在无噪声、有噪声且在线辨识、有噪声但不在线辨识三种情形下的系统误差对比