智能优化算法应用于Chen混沌系统参数辨识

Chen于1999年在混沌系统反控制的研究中发现了一个新的系统，随后，该系统被命名为Chen系统。该系统是一个非线性动力系统，表示为

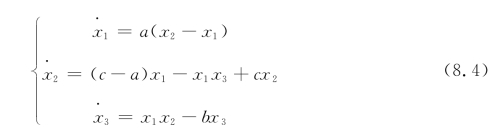
其中，当参数a=35，b=3，c=28时，式（8.4）所示的系统是混沌的。图8.4是Chen系统的演化过程。尽管Chen系统看上去与Lorenz系统结构相似，但实际上由于Chen系统比Lorenz系统多出一项，两者的拓扑结构并不等价。设Chen系统参数a，b，c未知，利用BFO算法进行参数辨识。

图8.4　Chen混沌系统

1.算法参数设置

所有算法的迭代次数设为200次，运行次数设为30次，变量范围a∈［20，50］，b∈［1，6］，c∈［10，40］。

BFO算法设置：细菌数为30，趋向次数Nc=40，复制次数Nre=4，迁徙次数Ned=2，游动次数Ns=3，游动步长C=0.001R（R为优化区间的宽度），迁徙概率Ped=0.25。

PSO算法设置：粒子数为30，惯性权重w=0.729，学习因子c1=c2=1.49，vmax=［30，3，30］。

GA算法设置：个体总数为30，交叉概率pc=0.8，变异概率pm随着种群向前进化，从0.01逐步增大至0.6，采取最优策略：将最优值直接传到下一代。(www.xing528.com)

2.算法参数设置

表8.2列出了三种算法对Chen系统参数辨识的结果。从表8.2中可以看出BFO算法得到的最优解是最好的，而且BFO算法的误差平均值小于另外两个算法，但标准偏差比PSO算法高。图8.5是三种算法的收敛曲线，可以看出PSO算法和BFO算法收敛速度和精度远远好于GA算法，一开始BFO算法的误差略高于PSO算法，但到了迭代后期BFO算法是三个算法中最好的。为了更好地对比三个辨识参数的结果，图8.6给出了不同参数和相应的实际值之间的相对误差。从图8.6可以看出，30次运行中，大多数情况下利用BFO算法辨识得到三个参数的相对误差都是最小的。

表8.2　三种算法的误差分析及最优解

图8.5　三种算法收敛速度比较

图8.6　Chen系统辨识参数与实际值的相对误差