【摘要】:设含有待辨识参数的动力学系统状态方程为其中,=(x1,x2,…,xn)T∈Rn是这个动力学系统的状态变量是状态变量的导数,θ=(θ1,θ2,…,xn),计算相应的误差作为细菌的适应值,即Step3寻优:对当前种群按照BFO算法寻优。系统的参数辨识问题转化为利用BFO算法搜索合适的参数)的数值,使得目标函数(8.2)全局最小化的问题。
设含有待辨识参数的动力学系统状态方程为
其中, =(x1,x2,…,xn)T∈Rn是这个动力学系统的状态变量
=(x1,x2,…,xn)T∈Rn是这个动力学系统的状态变量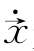 是状态变量
是状态变量 的导数,θ=(θ1,θ2,…,θm)是系统的未知参数。
的导数,θ=(θ1,θ2,…,θm)是系统的未知参数。
利用细菌觅食算法辨识参数θ=(θ1,θ2,…,θm)时,欲辨识参数为![]()
![]() ,菌群中的每一维即为需要辨识的参数,算法的步骤如下:
,菌群中的每一维即为需要辨识的参数,算法的步骤如下:
Step1 初始化:在每个参数的限定范围内随机产生初始种群中的N个个体Pi(i=1,2,…,N),t是迭代次数,每个参数取值的上、下限,一般根据已有和经验给定。
Step2 计算适应值:设第t代第i个个体Pi所对应的状态变量为(x1( ),
),![]() 。然后根据测得系统状态变量(x1(t),(x2(t),…,xn(t)),计算相应的误差作为细菌的适应值,即 (https://www.xing528.com)
。然后根据测得系统状态变量(x1(t),(x2(t),…,xn(t)),计算相应的误差作为细菌的适应值,即 (https://www.xing528.com)
Step3寻优:对当前种群按照BFO算法寻优。
Step4停止条件判断:若k≤MAXITER,则停止;否则k=k+1,回到Step2,
MAXITER为设定的最大迭代次数。
系统的参数辨识问题转化为利用BFO算法搜索合适的参数![]()
![]() )的数值,使得目标函数(8.2)全局最小化的问题。在数值仿真中利用Matlab程序采用四阶龙格—库塔算法求解常微分方程(8.1),步长h=0.01。利用BFO求解时,先让系统自由演化,在经历过一段暂态过程之后任意选取一点作为初值,并以此为0时刻,由此初值出发再任其演化至T=100h时刻,得到具有未知参数的动力学系统在离散时间序列0h,1h,…,100h上的一组标准状态变量值(x1(t),x2(t),…,xn(t))。
)的数值,使得目标函数(8.2)全局最小化的问题。在数值仿真中利用Matlab程序采用四阶龙格—库塔算法求解常微分方程(8.1),步长h=0.01。利用BFO求解时,先让系统自由演化,在经历过一段暂态过程之后任意选取一点作为初值,并以此为0时刻,由此初值出发再任其演化至T=100h时刻,得到具有未知参数的动力学系统在离散时间序列0h,1h,…,100h上的一组标准状态变量值(x1(t),x2(t),…,xn(t))。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




