智能优化算法应用实例

本节将在有测试噪声情况下，通过复合材料悬臂梁的数值模拟算例，来检验本章所提出的BFO—BP神经网络方法的优越性。这里，仅研究损伤定位。

首先，建立损伤位置的识别模式。利用有限元法将悬臂梁分为1～20总共20个单元，21个节点。如图7.6所示的一根矩形悬臂梁，结构完好时的参数如下：长200mm，截面宽10mm，高2mm；泊松比μ12=0.26，μ13=0.26，μ23=0.52；材料弹性模量E1=38.6GPa，E2=8.27GPa，E3=8.27GPa；剪切模量G12=4.14GPa，G13=4.14GPa，G23=3.10GPa；材料密度ρ=1033 kg/m3。结构的损伤其实质是结构局部刚度或质量的损失，假定结构某一单元的损伤只引起单元刚度的下降而不引起单元质量的改变，为了简化计算，通常假设结构的损伤是通过降低单元弹性模量E的方法进行模拟，并用弹性模量值EI的降低模拟实际结构中损伤单元的刚度下降。

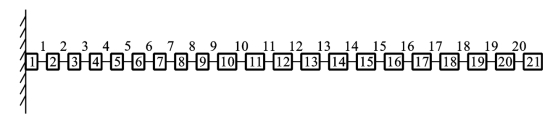
图7.6　复合材料悬臂梁结构的有限元模型

1.损伤位置模式样本的产生

采用图7.6中的有限元模型，以单元2、4、6、8、10、12、14、16、18共9个单元为例来模拟产生其损伤模式情况。

输入参数的选择对基于神经网络的结构损伤检测非常重要，输入参数应该选择对结构损伤比较敏感的特征因子。本节结合改进的损伤定位指标与标准化应变模态差的“组合损伤指标”作为网络的输入特征参数X，进行结构的损伤位置的识别。即式中，IFCRi（i=1，2，…，m）和NSMCj（j=1，2，…，n）分别为改进的损伤定位指标和标准化应变模态差指标。

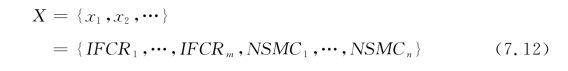
根据式（7.12），选取25个模态参数构成神经网络的输入向量，即悬臂梁的前5阶改进的损伤定位指标与20个标准化后的应变模态差指标。其中，20个标准化的应变模态差指标为第1阶应变模态在20个点处的损伤前后的标准化的应变模态差，这20个点是有限元模型中的第2～21节点。图7.7为9个损伤模式的无噪声标准化的应变模态差指标。表7.1为前5阶无噪声时改进的损伤定位指标。

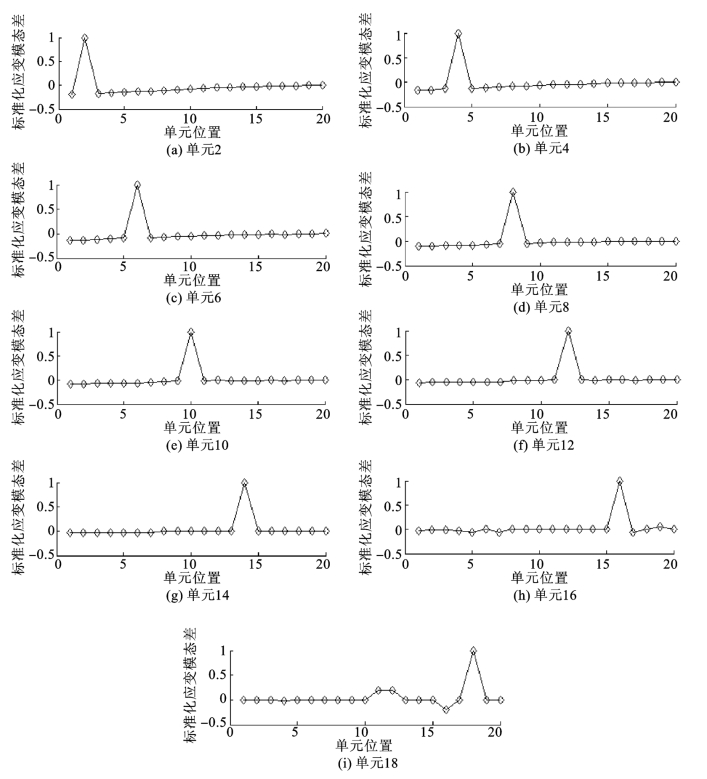
图7.7　9个损伤模式的标准化应变模态差曲线图

表7.1　前5阶无噪声时改进的损伤定位指标

为了得到训练样本，对每个模式计算相应的模态参数。由于测量误差是不可避免的，因而对每一个损伤序列在理论计算模态参数的基础上加一个相互独立的、正态分布的随机序列来模拟实测数据，即按式（7.13）进行模拟。(www.xing528.com)

式中，yi是叠加噪声后的测量模态参数（固有频率或模态矢量）；yai是某损伤模式类的理论分析模态参数；ε是损伤噪声程度指标；R是均值为0、偏差为1的正态分布随机数。对每一个损伤序列，随机产生100个测量数据集，一共产生100×9=900个训练样本。检验样本的产生方法与训练样本的产生方法一样，每个检验损伤序列产生100个测量数据集，共产生900个检验样本。训练样本和检验样本如表7.2所示。

表7.2　训练样本和检验样本

2.损伤定位的神经网络模型

如前所述，构造一个三层的BP网络，悬臂梁损伤定位的BP网络的输入层为前5阶改进的损伤定位指标和在20个点处的第1阶标准化应变模态差指标，其中神经元个数为25。每一个训练样本作为隐层中1个神经元，则隐层中神经元的数目为900。输出层有9个神经元，只有1个神经元的输出为1，其余的均为0。隐层采用式（7.6）中的S型激活函数，输出层采用线性激活函数purelin。

BP网络其他参数设置为：训练最大循环次数epoch=1000；期望最小训练误差goal=10-3；采用变学习速率BP算法。

BFO—BP网络采用和BP网络相同的网络结构和相同的参数设置，另外，取网络复制次数Nre=8；网络驱散概率ped=0.125。

3.损伤定位的识别结果

分别用BP网络模型和BFO—BP网络模型对噪声程度ε在1%～5%共五种情况下的损伤样本进行了损伤定位研究，识别结果如表7.3所示。

表7.3　BP网络模型和BFO—BP网络模型的识别结果

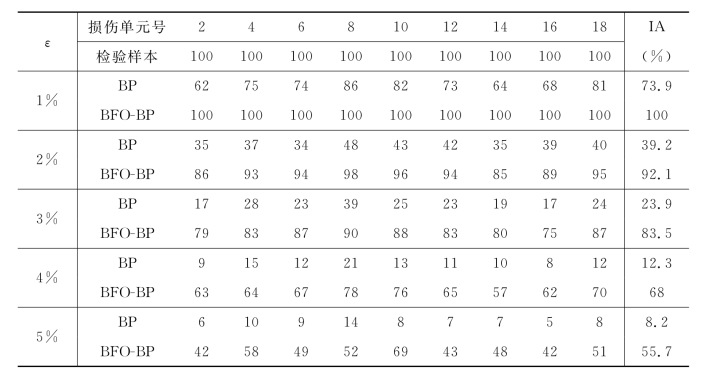
从表7.3中的网络仿真结果可以看出，在同一噪声水平情况下，相对BP网络而言，BFO—BP网络的损伤定位效果有较大优势。另外，对于这两种不同的网络模型来说，随着噪声的增大，损伤定位识别精度IA都减少。但与BP网络相比较，BFO—BP网络损伤位置识别的精度下降幅度较小，当ε=3%时，BFO—BP网络损伤定位识别结果仍具有较高精度（IA=83.5%），而此时，BP网络损伤定位的识别精度仅有23.9%。