智能优化算法：BP神经网络的理论与应用

BP（Error Back Propagation）神经网络是Rumelhart和McClelland于1986年提出的，且已成为至今应用最为广泛和成功的一种神经网络。网络不仅有输入层节点、输出层节点，而且还有隐含层节点（可以是一层或多层）。其上下层之间各神经元实现完全连接，即下层的每一个单元与上层的每一个单元都实现权连接，而每层各种神经元之间无连接。当一对样本学习模式提供给网络后，神经元的激活值从输入层经中间层向输出层传播，在输出层的各神经元获得网络的输入响应。在此之后，按减小希望输出与实际输出误差的方向，从输出层经各中间层逐层修正各连接权，最后到输入层。随着这种误差逆向传播修正的不断进行，网络对输入模式响应的正确率也不断上升。由于BP算法网络增加了中间隐含层并有相应学习规则可循，使其具有对非线性模式的识别能力，特别是对数学计算方法明确、步骤分明的学习，更具有广泛的应用前景。

典型的BP网络有三层，即输入层、隐含层（中间层）和输出层，各层之间实现完全连接，如图7.3所示。

隐含层神经元的激活函数一般选用式（7.6）中的S型函数。

BP网络训练是典型的有导师学习，其训练算法是对简单的δ学习规则的推广和发展。在BP网络训练过程中，输出层单元与隐含层单元的误差计算是不同的，最终的权值修正公式可以统一表示为

(www.xing528.com)

式中，wji和Δwji（t）分别为神经元j和i在时刻t的权值和权值变化量；η为网络学习率；oi为神经元i的输出；δj和netj分别为神经元j的误差和总输入；yj与oj分别为输出层神经元j的期望输出和实际输出。

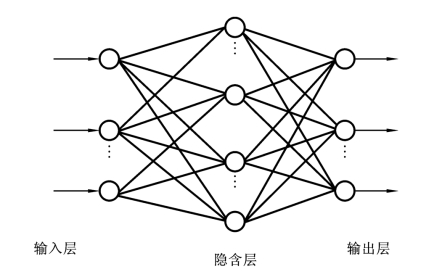
图7.3　三层BP网络结构图

尽管BP算法在网络训练过程中非常有用，但是该算法有两个主要缺陷：收敛缓慢和易陷入局部极小点。针对这一问题，目前国内外不少学者提出了许多改进算法。综合起来主要有三种：一是基于梯度下降法的改进，如动态算法、可变学习速度的反向传播算法和学习速率的自适应调节算法；二是基于数值计算的改进，如最小二乘法、牛顿法和LM算法等；三是混合算法，如BP算法和模糊算法、遗传算法、动态算法，或与其他算法的混合。