【摘要】:神经元不但是组成大脑的基本单元,而且也是大脑进行信息处理的基础元件。人们经过长期的研究总结出了神经元的几个重要特性,并据那些特性得到了如图7.1所示的生物神经元模型。图7.1神经元模型示意图神经元模型的数学表达式为式中,列向量X是输入向量,行向量Wj为单元j的连接权向量,Sj表示神经元的输入。
人的大脑由100亿~150亿个生物神经元构成,而其中的每一个神经元又与1万~10万个其他神经元相连接,如此构成了一个庞大的三维空间神经元网络(即神经网络)。神经元不但是组成大脑的基本单元,而且也是大脑进行信息处理的基础元件。所以,建立大脑的数学模型,必须从神经元入手。人们经过长期的研究总结出了神经元的几个重要特性,并据那些特性得到了如图7.1所示的生物神经元模型。图7.1中,f(˙)为非线性函数;x1,x2,…,xn为与神经元相关的n个输入信息;y1为输出结果;wj1,wj2,…,wjn为x1,x2,…,xn相应的权重系数;θj为输出阀值。
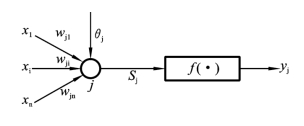
图7.1 神经元模型示意图
神经元模型的数学表达式为
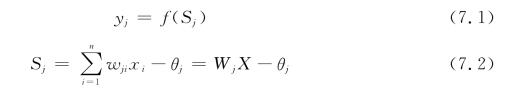
式中,列向量X是输入向量,行向量Wj为单元j的连接权向量,Sj表示神经元的输入。如果将阈值θj也视为神经元的第0个输入,其数值x0=-1,wj0=θj,则式(7.2)还可以表示为

非线性函数f(˙)称为激活函数,其作用是模拟生物神经元所具有的非线性转移特性。常用的激活函数有以下几种类型,如图7.2所示。
1.阈值型函数(https://www.xing528.com)

2.线性函数

3.S型函数
S型函数通常是在(0,1)或(-1,1)内连续取值的单调可微函数,常用指数函数或双曲正切函数。

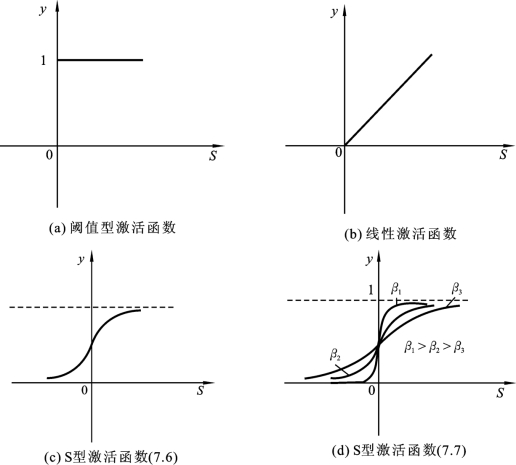
图7.2 神经网络激活函数图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




