智能优化算法:小生境遗传算法研究进展

小生境技术最先被用于遗传算法的改进研究。在自然界中，往往是特征、性状相似的物种聚集在一起，并在同类中交配并繁衍后代，但在基本遗传算法中，交配完全以随机的方式进行。虽然这种随机化的杂交形式在进化的初期保持了种群的多样性，但在进化后期会造成后代的近亲繁殖，从而降低进化的质量。为了解决随机杂交的有效性问题，自20世纪70年代以来，国内外的许多学者纷纷尝试在遗传算法中引入小生境技术，并已取得大量的研究成果。其中，最有代表性的小生境技术有以下几种：

1.基于预选择（Preselection）机制的小生境技术

Cavicchio于1970年率先在遗传算法中引入了基于预选择（preselection）机制的小生境技术。在这种预选择机制中，只有当子代个体的适应值超过其父代个体的适应值时，子代个体才能替换其父代个体而进入到下一代群体中，否则父代个体在下一代群体中继续保留。由于这种方式趋向于替换与自身因父子间的性状遗传而相似的个体，从而能够较好地维持群体的分布特性。Cavicchio声称采用基于预选择机制的小生境遗传算法可以在群体规模相对较小的情形下维持较高的群体分布特性，从而改进算法的搜索效能。

2.基于排挤机制（Crowding）的小生境技术

在生态学中，由于资源的有限，各种不同的生物为了能够在一个有限的生存空间中得以延续，不得不相互竞争。借鉴于该思想，1975年De Jong改进了Cavicchio的预选择机制，在其博士论文中提出了基于排挤机制（Crowding，也称为排挤因子模型）的小生境实现方法。主要步骤如下：

Step1　设定一个排挤因子（Crowding Factor，CF），并从当前群体中随机选取1/CF个个体组成排挤因子团体。

Step2　依据相似性原则，比较新产生的个体与排挤因子团体内的个体的相似性。

Step3　用新产生的个体去替换排挤因子团体中最相似的个体。

引入排挤机制的小生境遗传算法在优化的初始阶段，由于群体中个体间的相似性不存在显著差异，故个体的更新替换具有一定的随机选择特性。但在遗传优化的后期，群体中的个体逐步形成若干个小生境，此时基于个体相似性的替换技术可以在一定程度上维持群体的分布特性，并为进一步的分类和小生境的形成创造条件。De Jong曾将这一技术应用到多峰函数的遗传优化上，获得了比较满意的结果。但上述算法有个显而易见的缺陷，那就是排挤因子CF的取值不易掌握。若CF取值过大则影响算法的效率；而CF取值过小则会导致在搜索过程中部分峰值的丢失。

3.基于决定性排挤（Deterministic crowding，DC）机制的小生境技术

Cavicchio和De Jong声称这两种方法都可以在群体中形成小生境的进化环境，并维持了群体的多样性。但在相当长的时间里，对Reselection和Crowding的研究少之又少。直到1992年Mahfoud才又进行比较深入的研究，指出在实际应用中，这两种方法并不像其作者所声称的那样能成功地维持多样性，且对多模优化问题不能维持超过一个最优解。真实情况是这两种方法所采用的随机替代技术将产生大量的基因漂移，而使算法收敛于局部最优解。通过对Crowding方法的修改，Mahfoud提出了一种基于决定性排挤机制的小生境技术。该方法据说可以从根本上消除基因漂移。

DC可以看成是排挤算法的改进技术，其主要步骤为：

Step1建立初始群体P（0）。

Step2选择操作：从群体P（t）中随机选择两个父代个体P1和P2，并将其两两配对，若N为群体规模，则配对后将生成N/2对父代个体。

Step3对父代个体P1和P2进行交叉、变异或其他遗传操作，生成两个子代个体C1和C2。

Step4计算P1与C1、P2与C2、P1与C2、P2与C1的距离d1、d2、d3、d4。

Step5竞争与替代：若d1+d2≤d3+d4，则：

若f（c1）＞f（P1），用C1替代P1；

若f（c2）＞f（P2），用C2替代P2；

否则：

若f（c2）＞f（P1），用C2替代P1；(www.xing528.com)

若f（c1）＞f（P2），用C1替代P2；

其中，f（）为适应值函数。

DC具有算法简单、收敛速度快和隐含并行性等优点，被用于解决列车轨道混凝土的生产工艺问题，取得了较好的结果。

4.基于共享机制（Sharing）的小生境技术

小生境技术中最著名且用得最多的是1987年Goldberg和Richardson提出的基于适应值共享（Fitness Sharing）机制的小生境实现方法（简称FSGA）。算法认为每个小生境是有限的资源，在小生境中的个体将共享这个资源。在这个机制中，各个小生境中所有个体的适应值将按照物种规模以一定的比例降低，即通过反映个体之间相似程度的共享函数（sharing function）来调整群体中各个个体的适应值，从而在这以后的群体进化过程中，算法能够依据调整后的新适应值进行计算。共享函数是表示群体中两个个体i和j之间密切程度的一个函数，定义如下

式中，σ0（σ0＞0）为预先给定的小生境半径，dij为两个个体i和j之间的海明距离或欧氏距离，λ为共享程度参数。

由式（6.11）可知：

（1）0≤Sh dij≤1，Sh dij越大则两个个体之间关系越密切，也就是两个体间相似程度越大；反之，则两个个体之间相似程度不大。

（2）当dij=0时，Sh dij=1，即每个个体与自身的密切程度为1。

（3）当dij≥σ0时，Sh dij=0，即两个个体之间不密切相关，这表明两个个体处于不同的小生境中。

（4）当dij＜σ0时，在该范围内的个体小生境半径相同，信息共享，互相削减适应值，收敛在同一个小生境内。

（5）预先给定的小生境半径σ0是一个关键参数，直接影响到算法的搜索性能。因此需要先验知识来设定小生境半径σ0也是该算法最主要的缺陷。

1989年Deb和Goldberg给出小生境半径的设定方法，即

式中，k为优化问题的维度，m为优化问题最优解的个数。但该方法需要事先知道多峰值函数最优解的个数m，并且算法复杂度达到O（n2）——n为种群规模。1991年Oei介绍了几种降低算法复杂度的方法，主要是以在种群中选取若干个个体作为样本代替计算所有个体间的相似度，但每个小生境都要限定个体的最大数量。

在计算了个体之间的共享函数之后，就可以定义每个个体在群体中的共享程度——共享度了。它定义为该个体与群体内其他个体间共享函数值之和，用mi表示，即

式中，N是种群中所有个体的数目。由于当dij≥σ0时，Sh dij=0，个体i在整个种群中的共享度mi在数值上实际等于个体i在自身所在小生境中的共享度。

在计算了个体的共享度之后，再根据式（6.14）来更新个体的适应值，即

式中是第i个个体共享后的适应值，fi是第i个个体共享前的适应值。结合式（6.13）和式（6.14），可知：如果在一个小生境中包含了较多的个体，那么该小生境中所有个体经信息共享后共享度mi将大幅提高，而个体的适应值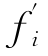将大幅降低，从而其他具有较少个体的小生境得以繁衍。

综上所述，基于适应值共享机制的小生境技术的基本思想可以概括为：将问题的解视为个体共享的资源，共享的方式是用个体的适应值除以共享度。对于比较稀疏的个体，其适应值的改变较小；而对于比较集中的个体，其适应值的改变较大。这样就可以限制种群内特殊物种的无限制增长，使稀疏的个体得以繁衍，从而维持种群的多样性。