1.求解TSP问题的人工鱼群算法步骤
求解TSP问题的人工鱼群算法实现的具体步骤如下:
Step1产生初始化种群:定义最大迭代次数num,拥挤度因子δ,视野范围visual,试探次数trynumber,并在可行域内随机生成N条人工鱼,形成初始鱼群。
Step2计算初始鱼群各人工鱼当前状态的值,比较其大小,最小值进入公告板,并且把对应的人工鱼状态赋值给公告板。
Step3按照人工鱼群算法的行为准则,进行追尾行为和聚群行为,缺省行为为觅食行为。如果进行了追尾行为和聚群行为后,最好值还是没有变化就进行随机行为。
Step4各人工鱼进行行为选择后,检查自身的值与公告板的值,如果优于公告板,则以自身取代,同时更新公告板上的人工鱼状态。
Step5判断是否满足终止条件,若不满足终止条件则转到Step3执行,进行下一步鱼群优化过程,否则转到Step6执行。
Step6算法终止,输出公告板上的最优解人工鱼群状态值。
2.算例及仿真研究
算法的参数取为最大试探次数为100,人工鱼个数为10,最大迭代次数取100,拥挤度因子0.8,感知范围为10,采用Matlab7.0为编程工具,实验环境为Intel(R)Core(TM)i3,2.13GHz CPU,2GB内存,Windows 7操作系统。为了便于比较,这项研究将人工鱼群算法与标准粒子群算法和基本遗传算法分别连续进行30次实验,对其结果进行比较分析。这项研究使用TSP问题中的标准测试算例TSPLIB库中的Oliver30(30个城市),Oliver30算例的目前已知最优解为423.7406。通过仿真实验对其结果进行比较分析,仿真结果如表5.4所示。(https://www.xing528.com)
标准粒子群算法中粒子数为100,惯性权重w从1.4线性递减到0.5,加速常数c1=c2=1.2,最大迭代次数为1000。遗传算法中,最大代数为1000,种群为100,交叉概率为0.8,变异概率为0.05,实验结果如表5.4所示,人工鱼群算法得到的最优路径如图5.6所示,寻优曲线如图5.7所示。算例Oliver30如下:
City[30]={{41,94},{37,84},{54,67},{25,62},{7,64},{2,99},{68,58},{71,44},{54,62},{83,69},{64,60},{18,54},{22,60},{83,46},{91,38},{25,38},{24,42},{58,69},{71,71},{74,78},{87,76},{18,40},{13,40},{82,7},{62,32},{58,35},{45,21},{41,26},{44,35},{4,50}}
表5.4 几种智能算法试验结果比较

由表5.4中的实验结果可知,人工鱼群算法得到的最优解为423.7406,与当前已知的Oliver30问题的最优解一致。标准粒子群算法的最优解为425.5416,遗传算法的最优解为424.6918,都没有收敛到当前最优解。根据图5.6可知,人工鱼群算法求得的最优路径也与已知的最好解对应的路径是一致的。

图5.6 Oliver30问题最优路径
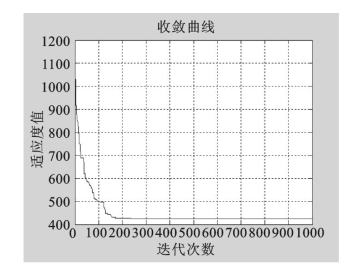
图5.7 Oliver30问题寻优曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




