本节给出一种新颖的基于粒子群优化求解车间作业调度问题的算法。为了适合于JSSP的求解,拓广了粒子群系统中粒子的距离和速度的含义。提出的基于粒子群优化的车间作业调度算法有效地利用了粒子群系统的分布和并行计算的性能。对调度标准测试问题进行了模拟实验,结果表明该算法能够比较有效地获得问题的近似优化解。
1.粒子群系统中JSSP的表述
用粒子群算法解决JSSP,每个粒子代表问题的一个潜在解,也就是一个可行调度.本节采用了一种基于操作(工序)的编码方式,每个粒子由n×m个代表操作的基因组成,是所有操作的一个排列,其中,各工件号均出现m次,自左向右扫描该排列,某个工件号的第k次出现表示该工件的工艺约束中的第k道工序。
例如,对于一个4×4调度问题(4个工件,4台机器),假如粒子群系统中的一个粒子为(2 1 3 4 2 4 3 2 1 2 3 3 1 1 4 4)。由于每个工件包含4个操作,因此,工件号重复出现4次,其中,粒子的第5个基因2,由于是工件2在整个排列中自左向右扫描时第2次出现,故它表示工件2的第2道工序。类似地,第8个基因表示工件2的第3道工序,依此类推。
容易注意到,这种编码方式的显著优点是任意基因串的置换排列均能表示可行调度,而且解码时避免了死锁的发生;其缺点是使解空间产生了冗余性,即代表粒子的码与调度是多对一的关系,对于n×m问题,粒子的搜索空间增长为(n×m)!(m!)n。同时,这种编码方式具有半Lamarkian性和1类解码复杂性,其中,半Lamarkian性是指后代所继承的码的片段中只有部分与父代相同,1类解码复杂性是指通过简单映射关系即可实现解码。
2.初始粒子群生成
若随机生成粒子群系统中的初始粒子,整个搜索过程相对要花费较长的时间,而且降低了获得最优解的可能性。本节利用Giffler-Thompson算法产生初始群体,该算法是一种生成活动调度的树搜索算法。其步骤如下:
Step1令Q(1)={Oij|i=l,2,…,n;j=1,2,…,m}为所有操作的集合;S(1)为所有工件第1道工序的集合。
Step2令t=1。
Step3令o*为满足c(o*)=min{c(oij)|oij∈S(t)}的操作,m*为进行该操作的机器;从集合{oim*S(t);r(oim*)<c(o*)}中确定一个操作oim*。
Step4生成Q(t+1)=Q(t)\{oim*}。由S(t)除去操作oim*,并添加工件i的下一道工序来生成集合S(t+1)。
Step5若Q(t+1)为非空,则令t=t+l,并转Step3;否则结束算法。
其中,oij表示工件i在机器j上的操作,pij表示oij的加工时间,S(t)表示第t步的前一道工序执行时刻所有未执行操作的集合,r(oij)表示S(t)中的oij对应的工件i到达机器j的时间,c(oij)表示S(t)中的oij可完成的最早时间,即c(oij)=r(oij)+pij。
3.目标函数和适应度函数
最常用的JSSP的目标函数是最小化最大完工时间,即makespan。在数学上,JSSP是为了寻找这样一个调度
![]()
其中,T(i)是机器i上所有工件的最终完成时间,T(JM)是所有工件的最终完成时间。
粒子的适应度用下面的公式进行评估

其中,fi为第i个粒子的适应度,opt为问题已知的最优解.目标函数值Ti(JM)可以通过解码操作获得。由于最优解一定是活动调度,本节采用活动化解码操作,这样可以使粒子解码后所得到的最大完工时间最小化。
设粒子群中每个粒子结构形如a[1],a[2],…,a[n×m],其中,a[1]∈{1,2,…,n},i=l,2,…,n×m。活动化解码算法如下:
Stepl 令k[i]=l,i=l,2,…,n。
Step2 For i=1 to n×m。
(1)得到加工工件a[i]机器号JM(a[i],k[a[i]]);
(2)令k[a[i]]=k[a[i]]+1;
(3)将工件a[i]在机器JM(a[i],k[a[i]-1)上的操作以最早允许加工时间加工,即从零时刻到当前时刻对该机器上的各加工空闲依次判断能否将此工件插入加工。若能,则在空闲中插入加工,并修改该机器上的加工队列;否则,以当前时刻加工该工件,将此工件排在当前队列的末尾。
算法中,工序I能在空闲时间段[t1,t2]插入加工的条件为
![]()
其中,t1和t2分别为空闲起始和终止时刻,t(I)为工序I目前的最早允许加工时间,TI为工序在机器上的加工时间。
例如,考虑表4.5中的三个工件,两个机器的调度问题。该问题中工件1首先要在机器2上加工一个单位时间,继而在机器1加工两个单位时间,依此类推。假设一个粒子为a=(1,3,2,2,l,3),它对应的半活动调度的Gantt图如图4.4所示,其makespan为7个单位时间,而它对应的活动调度的Gantt图如图4.5所示,其makespan为6个单位时间,
表4.5 3×2调度实例

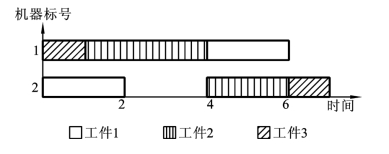
图4.4 半活动调度Gantt图
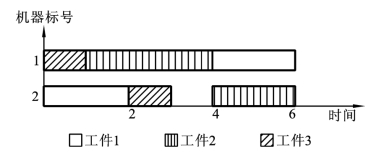
图4.5 活动调度Gantt图
4.冗余性与二级编码(https://www.xing528.com)
注意到,粒子群系统中每个粒子对应唯一一个活动调度,而一个调度可能对应多个相同的粒子,也就是说,粒子的搜索空间存在冗余性,仍以粒子a=(1,3,2,2,1,3)为例,显然,存在一个粒子b=(3,2,1,2,1,3)。
通过从左向右依次扫描一个粒子的所有基因,可以按顺序得到在某一个机器上加工的所有工件编号。对每个机器重复这样的操作,可以得到一个新的排列,这里将这个排列称为粒子的二级编码(bilevel encoding)。如果两个粒子的二级编码相同,则它们对应同一个调度。上述的粒子a和b的二级编码均为(3,2,l,l,2,3),故它们对应同一个调度,称粒子a和b具有冗余性。如果一个粒子具有亢余性,随机交换它的两个不同的基因。二级编码的目的只是为了降低搜索空间的冗余性,在粒子群系统的其余操作中,仍采用基于工序的表述方式。
5.粒子群系统的更新方式
由于传统的粒子群优化算法不能直接用于求解车间作业调度问题,为了适合于JSSP的求解,拓广了粒子群系统中粒子的距离和速度的含义,并提出了一种用于求解JSSP的离散粒子群优化算法。首先给出两个粒子的相似度的定义,设xi=(xil,xi2,…,xiD)和xj=(xjl,xj2,…,xjD)分别表示D维空间的第i个和第j个粒子,定义函数
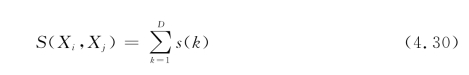
其中
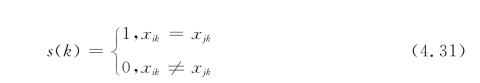
称S(Xi,Xj)为粒子Xi和粒子Xj的相似度。
两个粒子之间的距离用下面的公式进行定义
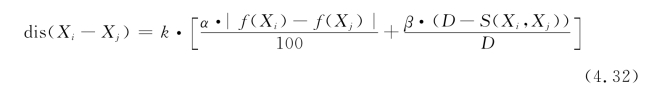
其中,f(Xi)和f(Xj)分别为粒子Xi和粒子Xj的适应度,D是粒子的维数,k是一个称为加速系数的正整数,α和β是两个正的权值,它们可以通过尝试来确定,并且满足α+β=1,本节的模拟实验中α和β分别取值0.6和0.4。显然0≤|f(Xi)-f(Xj)|/100≤1,0≤(D-S(Xi,Xj))/D≤1。
相应地,也将粒子的速度的含义拓广为基因置换的次数。设X=(x1,x2,…,xD)和Y=(y1,y2,…,yD)分别表示D维空间的两个粒子,一次基因置换的具体方法如下:
(1)设置计数器m=0,随机选择两个粒子的第k个基因,如果xk=yk=s,转(2);否则,即xk=s,yk≠s转(3),其中,s是粒子第k个基因对应的工件号。
(2)分别从左至右扫描粒子X和Y的第k个基因以前的基因片段,并记录s出现的次数,分别标注为XT(s,k)=tx,YT(s,k)=ty。如果tx>ty,转(4);如果tx<ty,转(5);否则,即tx=ty,转(6)。
(3)随机选粒子Y的第j个基因,直到满足yj=s,yj≠cj。交换基因yj和yk,并设置计数器m=l,转(2)。
(4)在粒子Y中,随机选择第k个基因以前的满足条件yj≠cj,yj≠s,j<k的基因,将该基因同Y中出现在第k个基因以后的代表工件号s的基因交换位置,直到tx=ty,转(7)。
(5)在粒子Y中,随机选择第k个基因以后的满足条件yj≠xj,yj≠s,j>k的基因,将该基因同Y中出现在第k个基因以前的代表工件号s的基因交换位置,直到tx=ty,转(7)。
(6)如果m=0,重新随机选取基因位置标号k,1≤k≤n×m;如果m=l,转(7)。
(7)算法结束。
用“①”标注基因的置换操作,提出的适用于求解车间作业调度问题的粒子群优化算法的更新公式可以表示为
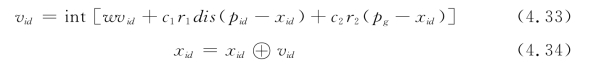
其中,int[˙]表示取整函数,dis(˙)可以通过式(4.32)求得。
6.基于粒子群优化求解JSSP的流程
粒子在按粒子群系统更新式(4.33)和式(4.34)进行更新后,进行两种提出的启发式操作——局部搜索和阶跃记忆回溯,以加速算法的收敛速度。
局部搜索是指对于每个粒子随机进行k位调整以寻求更优解,0≤k≤bit,其中,bit为调整位数的上限。k位调整通过选择粒子中的k个位置并随机交换这些位置上的基因来完成操作。调整操作后用新产生的粒子来替换原来群体中的最差粒子。
阶跃记忆回溯具体描述如下:
粒子群系统每隔g代进行一次群体记忆,g的大小随着当前迭代次数NG的增加每隔一定代数而呈阶跃式增加,具体表示为
![]()
其中,t的初始值为1,每发生一次阶跃,g与当前迭代次数NG的关系如图4.6所示,其中,散点表示记忆时间。
这样粒子群系统具有保留过去某时间段的整个群体快照,同时为节省储存空间,设粒子群系统的记忆深度为3,也就是说,它只能保留最近三次的群体快照。如果粒子群中的最优粒子gbest在一定次数的迭代过程中没有改善,在保留最优粒子的前提下,按一定的比率随机从三次快照中引入部分粒子替代群体中的部分粒子。
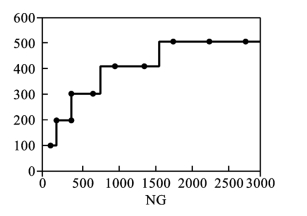
图4.6 g与当前迭代次数NG的关系
基于粒子群优化求解JSSP的流程图如图4.7所示。
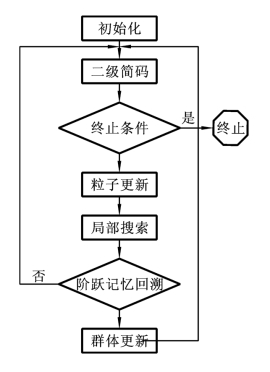
图4.7 基于粒子群优化求解JSSP的流程框图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




