智能优化算法:粒子群优化与混沌理论的结合

1.基本粒子群优化算法的不足

分析基本粒子群优化算法搜索过程有两点不足：

（1）初始化过程是随机的，随机过程虽然大多可以保证初始解群分布均匀，但对个体的质量不能保证，解群中有一部分远离最优解。如果初始解群比较好，将会有助于求解效率与解的质量。

（2）利用式（4.1）、式（4.2）更新自己的速度和新的位置，本质是利用本身信息、个体极值信息和全局极值三个信息，来指导粒子下一步迭代位置。这实际上是一个正反馈过程，当本身信息和个体极值信息占优势时，该算法很容易陷入局部最优解。

2.混沌粒子群优化算法（CPSO）的基本思想

将混沌引入粒子群优化算法就是对基本粒子群优化算法的不足提出改进，基本思路是：利用混沌运动的遍历性，产生大量初始群体，从中择优出初始群体；对当前粒子个体产生混沌扰动，以使解跳出局部极值区间。

设求解n维的优化问题：

解优化问题的混沌粒子群优化算法步骤如下：

（1）混沌初始化。随机产生一个n维、每个分量数值在0～1之间的向量z1=（z11，z12，…，z1n）。根据式（3.20），zi+1j=μzij（1-zij）（j=1，2，…，n；i=1，2，…，N-1）得到N个z1，z2，…，zN。将zi的各个分量载波到优化变量的取值范围：xij=aj+（bj-aj）zij（j=l，2，…，n；i=1，2，…，N）。计算目标函数，从N个初始群体中选择性能较好的m个解作为初始解，随机产生m个初始速度。

（2）根据当前位置和速度产生各个粒子的新的位置。

（3）随机产生一个n维、每个分量数值在0～1之间的向量u0=（u01，u02，…，u0n）。

While（迭代次数k＜规定迭代次数nmax）do

For i=l：m

（4）按式（4.1），更新自己的速度，并把它限制在vmax内。

（5）根据式（3.20），产生u1=（u11，u12，…，u1n），u1j=4u0j（1-u0j）（j=1，2，…，n），将u1的各个分量载波到混沌扰动范围［-β，β］内，扰动量△x=（△x1，△x2，…，△xn）为△xj=-β+2βu1j，u0=u1；xik+1=xik+vik+1，=xik+vik+1+Δx，计算这两个位置的适应值f和f＇。若f＇＜f，则xik+1=。

（6）k=k+l，计算第i个粒子的适应值fi。若粒子的适应值优于原来的个体极值，设置当前适应值为个体极值pfbestik，设置当前位置为个体极值位置pxbestik。

（7）根据各个粒子的个体极值pfbesik（i=1，2，…，m），找出全局极值gfbesk和全局极值位置gxbesk。

输出全局极值gfbest和全局极值位置gxbest。(www.xing528.com)

3.算法测试

（1）迭代次数测试

用CPSO对以下4个经常被国内外学者用来测试优化算法有效性的测试函数进行优化计算，以精度为0.00001时所需要的迭代次数作为比较。初始群体数N=100，粒子数m=50，每种算法运行100次，结果如表4.3所示。

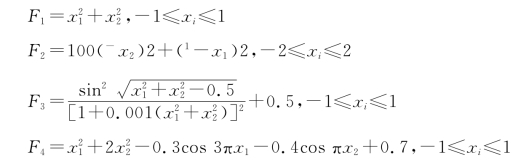
表4.3　迭代次数结果比较

CPSO算法是指在基本粒子群优化算法上加入混沌初始化和混沌扰动。从表4.3中可以看出基本粒子群优化算法上加入混沌初始化或混沌扰动后，大多数情况效果比较好，少数情况效果稍差的原因是加入混沌后，搜索的区域较大，有可能使迭代次数增加。同时加入混沌初始化和混沌扰动的混沌粒子群优化算法的效果更好，迭代次数明显减少。

（2）收敛性测试

同样以上述4个函数为测试函数，初始群体数N=100，粒子数m=50，以最大迭代次数100次为停止条件，每种算法运行100次，计算平均最优解，结果如表4.4所示。从表4.4中可以看出基本粒子群优化算法容易陷入局部最优，加入混沌初始化或混沌扰动后，或同时加入混沌初始化和混动扰动，某种程度上可以跳出局部最优解。

表4.4　平均最优解比较

（3）与前人的研究成果比较

为了更一步验证方法的有效性，考虑下面优化问题：

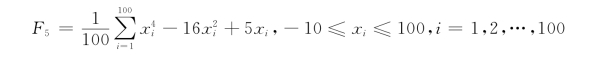
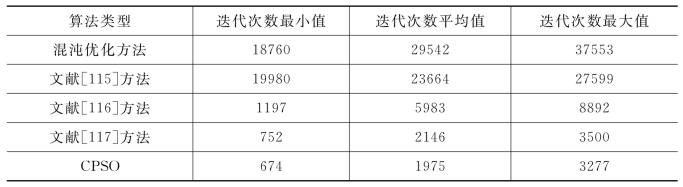
当xi*=-2.904时，该函数的最小目标值为-78.3323，与前人的研究成果进行比较，每种算法均运行10次，结果如表4.5所示，从表4.5中可以看出本项目的混沌粒子群优化算法的有效性。

表4.5　与其他文献的结果比较