基本粒子群优化算法中，虽然粒子速度作了限制，不会变化太大，但位置更新时未作限制，就有可能新的位置会变得很坏，引起收敛速度缓慢，所以要对更新的位置作限制。限制的思路有两种方法：一种采用类似于速度限制的方法，给每一维变量限制一个范围。具体修改如下：
方法1 其他步骤同基本粒子群优化算法的程序，步骤（5）变为：“按式（4.2），更新当前的位置，并把它限制在xmax内”。
另一种思路采用模拟退火算法思想，模拟退火算法用于优化问题的出发点是基于物理学中固体物质的退火过程与一般优化问题的相似性。算法的基本思想是从一给定解开始的，从邻域中随机产生另一个解，接受准则允许目标函数在有限范围内变坏，以一定概率接受新的解。因此有3种方法改进分述如下。
方法2 按式（4.2），计算新的位置，计算两个位置所引起的适应值的变化量△E；若△E≤0，接受新值，否则若exp（-△E/T）＞rand（0，1）（rand（0，1）表示0～1之间的随机数），也接受新值；否则就拒绝，xk+1仍为xk。具体步骤如下：
（1）对每个粒子初始化，设定粒子数n，随机产生n个初始解或给出n个初始解，随机产生n个初始速度，给定起始温度T、终止温度T0和退火速度α。
（2）根据当前位置和速度产生每个粒子的新位置。
While（迭代次数＜规定迭代次数）do
（3）计算每个粒子新位置的适应值；对每个粒子，若粒子的适应值优于原来的个体极值pbest，设置当前适应值为个体极值pbest。
（4）根据各个粒子的个体极值pbest找出全局极值gbest。
（5）按式（4.1），更新自己的速度，并把它限制在vmax内。
（6）按式（4.2），更新当前的位置。
（7）计算两个位置所引起的适应值的变化量△E；若△E≤0，接受新值；否则若exp（-△E/T）＞rand（0，1）（rand（0，1）表示0～1之间的随机数），也接受新值：否则就拒绝，xk+1仍为xk。
（8）若接受新值，降温T←αT；否则不降温。
方法3 接受准则允许目标函数在有限范围内变坏，且不按概率取舍，直接按△E＜e，e为按允许目标函数变坏范围。具体算法如下：
（1）对每个粒子初始化，设定粒子数n，随机产生n个初始解或给出n个初始解，随机产生n个初始速度。
（2）根据当前位置和速度产生各个粒子的新的位置。
While（迭代次数＜规定迭代次数）do
（3）计算每个粒子新位置的适应值。
（4）对各个粒子，若粒子的适应值优于原来的个体极值pbest，设置当前适应值为个体极值pbest。(www.xing528.com)
（5）根据各个粒子的个体极值pbest找出全局极值gbest。
（6）按式（4.1），更新自己的速度，并把它限制在vmax内。
（7）按式（4.2），更新当前的位置。
（8）计算两个位置所引起的适应值的变化量△E；若△E＜e，e为按允许目标函数变坏范围△E≤0，接受新值；否则就拒绝，xk+1仍为xk。
方法4 将方法1与方法3结合在一起，其他步骤同方法3，Step7变为：“按式（4.2）式，更新当前的位置，并把它限制在xmax内”。
2.算法测试
在本节中，以一个简单的优化问题min f（x1，x2）=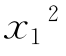
+
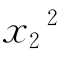来测试各种算法。
在基本粒子群优化算法中，粒子数n=4，c0=l，初始粒子位置为（2，1）、（-1，3）、（-1.5，-1）、（1.5，-1.5），vmax=5，初试速度都为0。
方法1的参数与基本粒子群优化算法相同，xmax=10。
方法2的参数与基本粒子群优化算法相同，起始温度T=100000，退火速度α=0.99。
方法3的参数与基本粒子群优化算法相同，e=100。
方法4的参数与基本粒子群优化算法相同，e=100，xmax=10。
测试的优化问题解为（x1*，x2*）=（0，0），fmin=0。以目标函数f＜0.01为停止条件，测试两种达到要求的迭代次数为衡量标准。各种算法各随机测试100次，结果如表4.2所示。
方法1比基本粒子群方法有所改进。方法2不如方法3和方法4。因为方法2中，随着温度的降低，接受的概率变得很小，可能使有些粒子的位置停止不前，反而使收敛速度很慢。从表4.2中可以看出，方法4算法是一种比较有效的算法，图4.3是方法4在x1-x2二维空间的迭代游历图。
表4.2 各种策略测试结果
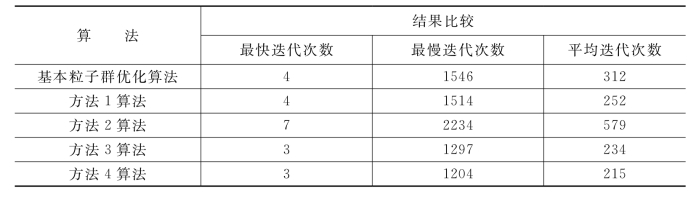
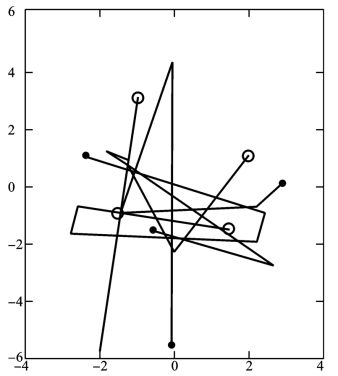
图4.3 方法4的迭代过程
（○表示起始点，●表示终点）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
