收敛性分析-智能优化算法书籍

从式（4.3）、式（4.2）可以看出，尽管vk和xk是多维变量，但每维相互独立，故对算法分析可以简化到一维进行，为简化计算，并且假设粒子本身所找到的最优解的位置和整个种群目前找到的最优解的位置不变，记为pb和gb，c0（记c0=w）、c1和c2为常数。式（4.3）、式（4.2）可以简化为

由式（4.6）和式（4.7）可得

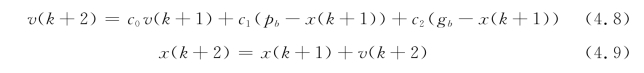
将式（4.7）和式（4.8）代入式（4.9）得

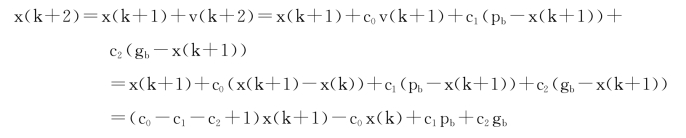
即

这是二阶常系数非齐次差分方程，解此差分方程方法较多，最典型的方法是特征方程方法。

首先解式（4.10）的特征方程：λ2+（c0+c1+c21）λ+c0=0，根据一元二次方程解的情况分3种情况：

（1）当Δ=（-c0+c1+c2-1）2-4c0=0时，λ=λ1=λ2=-（-c0+c1+c2-1）/2，此时x（k）=（A0+A1k）λk，A0、A1为待定系数，由v（0）和x（0）确定。经计算得

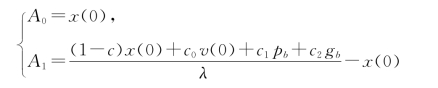
（2）当Δ=（-c0+c1+c2-1）2-4c0＞0时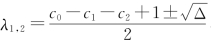，，此时x，A0、A1、A2为待定系数。(www.xing528.com)

令b1=x（0）-A0，b2=（1-c）x（0）+c0v（0）+c1pb+c2gb-A0，经计算得到

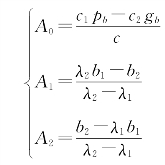
（3）当Δ=（-c0+c1+c2-1）2-4c0＜0时，，此时，A0、A1、A2为待定系数。类似可得

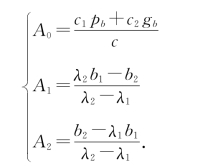
当k→∞时，x（k）有极限，趋向于有限值，表示迭代收敛。由此可知，若要求上述三种情况x（k）收敛，其条件是：‖λ1‖＜1且‖λ2‖＜1。

经过计算可得以下结论，令c=c1+c2：

当△=0时，收敛区域为：抛物线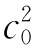+c2-2c0c-2c0-2c+1=0且0≤c0≤1。

当△＞0时，收敛区域为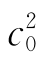+c2-2c0c-2c0+1＞0且c＞0和2c0-c+2＞0所围成的区域。

当△＜0时，收敛区域为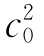：+c2-2c0c-2c0-2c+1＜0和c0＜1所围成的区域。

综合上述三种情况，收敛区域为c0＜1，c＞0和2c0-c+2＞0所围成的区域，如图4.2所示。

图4.2　收敛区域