智能优化算法理论与应用：粒子更新的原理

PSO算法源于对鸟群捕食行为的研究，一群鸟在随机搜寻食物，如果这个区域里只有一块食物，那么找到食物的最简单有效的策略就是搜寻目前离食物最近的鸟的周围区域。PSO算法就是从这种模型中得到启示而产生的，并用于解决优化问题。在该算法中，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”。所有的粒子看成搜索空间中没有质量和体积的点，而且都有一个适应值，这个适应值根据被优化的函数确定。每个粒子都有自己的位置和速度以决定它们飞翔的方向和距离，PSO算法通过将解空间初始化为一群随机粒子（随机解），然后经过迭代找到最优解。在每一次迭代中，粒子通过两种经验来更新自己。一种是自己的飞行经验，也就是粒子经历过的最好位置（最好的适应值），即本身所找到的最优解，称为“局部最优pbest”；另一种是同伴的飞行经验，也就是群体所有粒子经历过的最好位置，即整个种群目前找到的最优解，称为“全局最优gbest”。

设目标搜索空间为D维，粒子的群体规模为m。在找到上述两个最好解后，粒子根据式（4.1）和式（4.2）来更新自己的速度和位置。设粒子i的位置表示为xi=（xi1，xi2，…，xiD）T，速度为vi=（vi1，vi2，…，viD）T，则速度和位置更新方程为

其中，i=1，2，…，m；d=1，2，…，D；k是迭代次数；rand1，rand2是［0，1］之间的随机数；c1，c2是学习因子，也称为加速因子，它们使粒子具有自我总结和向群体中优秀个体学习的能力，分别调节粒子向全局最优gbest和局部最优pbest方向飞行的最大步长，这两个参数对粒子群优化算法的收敛起的作用不是很大，但合适的c1，c2可以加快收敛且不易陷入局部最优，通常令c1=c2=2.0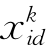；和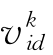分别是粒子i在第k次迭代中第d维的当前位置和速度；是粒子i在第k次迭代中第d维的个体极值点的位置是整个群在第k次迭代中第d维的全局极值点的位置。由于PSO算法中没有实际的机制来控制粒子速度，为防止粒子远离搜索空间，粒子的每一维速度vd都会被限制在［-vdmax，vdmax］之间，参数vdmax被证明是非常重要的，vdmax太大，粒子将飞离最好解，太小将会陷入局部最优。

式（4.1）的第一部分为粒子先前的速度；第二部分为“认知”部分，表示粒子对自身的学习；第三部分为“社会”部分，表示粒子间的信息共享与相互合作。式（4.1）正是粒子根据它上一次迭代的速度、粒子当前位置和自身最好经验与群体最好经验之间的距离来更新速度。然后粒子按照式（4.2）飞向新的位置。

为了改善基本粒子群优化算法的收敛性，Shi和Eberhart［1］于1998年在IEEE国际进化计算学术会议上提出了带惯性权重的PSO算法，即添加一个惯性权重到速度更新公式（4.1），按下式更新速度

其中，w称为惯性权重系数，它起着权衡全局优化能力和局部优化能力的作用。位置更新公式仍为式（4.2）。

由于速度更新公式（4.3）是标准PSO算法的核心，下面将通过对该式的进一步分析与讨论来充分了解标准PSO算法的本质。

1.如果粒子群速度公式（4.3）中没有第一部分（称为惯性项），即w=0，则速度只取决于粒子当前位置和历史最佳位置（pbest和gbest），速度本身没有记忆性。假设一个粒子位于全局最优解的位置，它将保持静止，而其他粒子则飞向它本身最佳位置pbest和全局最优解位置gbest的加权中心。在这种条件下，粒子仅能探测有限的区域，更像一个局部算法。惯性项的作用在于赋予各粒子扩展搜索全空间的能力，即全局搜索能力。这种功能使得调整w的大小可以起到调整算法全局和局部搜索能力权重的作用。

2.如果粒子群速度公式中没有后两部分，即c1=c2=0，粒子将在惯性因子w的作用下，从初始速度v0开始飞行。这时将出现以下三种情况：(www.xing528.com)

（1）如果w＞1.0，则当前速度始终是初始速度的放大；

（2）如果w＜1.0，则当前速度从初始速度开始，成几何级数衰减；

（3）如果w=0，则粒子一直以初始速度飞行，不会改变飞行的方向和速度的大小，将很快飞出可行域的边界。这种情况下，粒子将很大可能搜索不到优解，除非优解恰好落在粒子飞行的轨迹上，显然这种事件是极小概率事件。

无疑，上述这三种情况对最优解的搜索都是不利的。要么粒子按照固定的方向飞行，可能很快飞出可行域的边界；要么粒子的速度在短时间内衰减趋于0。这三种情况中，粒子的搜索区域都受到很大的限制，所以很难找到最优解。

3.如果式（4.3）中没有第二部分，即c1=0，则粒子没有个体认知能力，也就是“只有社会认知”的模型。在粒子的相互作用下，虽然可能探索新的解空间，但对稍微复杂的问题很容易导致“盲从”而陷入局部极值点。

4.如果式（4.3）中没有第三部分，即c2=0，则粒子之间没有社会信息共享，也就是“只有个体认知”的模型。因为个体间没有信息交互，一个规模为m的群体等价于执行了m个粒子的单独搜索，因而得到最优解的概率大大减小。

自从Shi和Eberhart提出以上带惯性权重的PSO算法后，人们逐渐地都默认这个改进PSO算法为标准的PSO算法。