连续域蚁群优化算法的改进方法

许多工程中的实际问题通常表达为一个连续的最优化问题，并随着问题规模的增大以及问题本身的复杂度增加，对优化算法的求解性能提出越来越高的要求。而基本蚁群优化算法优良高效的全局优化性能却只能适用于离散的组合优化问题。因为基本蚁群优化算法的信息量留存、增减和最优解的选取都是通过离散的点状分布求解方式来进行的，所以基本蚁群优化算法从本质上只适合离散域组合优化问题，离散性的本质限制了其在连续优化领域中的应用。在连续域优化问题的求解中，其解空间是一种区域性的表示方式，而不是以离散的点集来表示的。因此，将基本蚁群优化算法寻优策略应用于连续空间的优化问题需要解决以下三点。

1.调整信息素的表示、分布及存在方式

调整信息素的表示、分布及存在方式是至关重要的一点，在组合优化问题中，信息素存在于目标问题离散的状态空间中相邻的两个状态点之间的连接上，蚂蚁在经过两点之间的连接时释放信息素，影响其他蚂蚁，从而实现一种分布式的正反馈机制，每一步求解过程中的蚁群信息素留存方式只是针对离散的点或点集分量；而用于连续域寻优问题的蚁群优化算法，定义域中每个点都是问题的可行解，不能直接将问题的解表示成为一个点序列，显然也不存在点间的连接，只能根据目标函数值来修正信息量，在求解过程中，信息素物质则是遗留在蚂蚁所走过的每个节点上，每一步求解过程中的信息素留存方式在对当前蚁群所处点集产生影响的同时，对这些点的周围区域也产生相应的影响。

2.改变蚁群的寻优方式

由于连续域问题求解的蚁群信息留存及影响范围是区间性的，非点状分布，所以在连续域寻优过程中，不但要考虑蚂蚁个体当前位置所对应的信息量，还要考虑蚂蚁个体当前位置所对应特定区间内的信息量累计与总体信息量的比较值。

3.改变蚁群的行进方式

将蚁群在离散解空间点集之间跳变的行进方式变为在连续解空间中微调式的行进方式，这一点较为容易。

近年来，随着蚁群优化算法的不断改进，拓展蚁群优化算法的功能，使之适用于连续问题已经有了一些成果，分为以下三类。

（1）将蚁群优化框架与进化算法结合，从而实现连续优化算法。

第一个连续蚁群优化算法是由Bilchev G A等学者基于这种思路构建的，求解问题时先使用遗传算法对解空间进行全局搜索，然后利用蚁群优化算法对所得结果进行局部优化，但这种算法在运行过程中常会出现蚂蚁对同一个区域进行多次搜索的情况，降低了算法的效率；杨勇等学者提出了一种求解连续域优化问题的嵌入确定性搜索蚁群优化算法，该算法在全局搜索过程中，利用信息素强度和启发式函数确定蚂蚁移动方向，而在局部搜索过程中嵌入了确定性搜索，以改善寻优性能，加快收敛速度。

（2）将连续空间离散化，从而将原问题转化为一个离散优化问题，然后应用基本蚁群优化算法的原理来求解。

高尚等学者提出了一种基于网格划分策略的连续域蚁群优化算法；汪镭等学者提出了基于信息量分布函数的连续域蚁群优化算法；李艳君等学者提出了一种用于连续域优化问题求解的自适应蚁群优化算法；段海滨等学者提出了一种基于网格划分策略的自适应连续域蚁群优化算法；陈峻等学者提出了一种基于交叉变异操作的连续域蚁群优化算法等。采用这种方式来研究的比较多，但当问题规模增大时，经离散化后，问题的求解空间将急剧增大，寻优难度将大大增加。对于较大规模的连续优化问题这类方法的适应性还有待进一步的验证。

（3）对蚂蚁行为模型进行更加深入的、广泛的研究，从而构造新的蚁群优化算法，应用于连续问题的求解。

Dréo J等学者提出了一种基于密集非递阶的连续交互式蚁群优化算法CIACA，该算法通过修改信息素的留存方式和行走规则，并运用信息素交流和直接通信两种方式来指导蚂蚁寻优；Pourtakdoust S H等学者提出了一种仅依赖信息素的连续域蚁群优化算法；张勇德等学者提出了一种用于求解带有约束条件的多目标函数优化问题的连续域蚁群优化算法。

由于篇幅所限，这里不能一一列举，仅介绍两种，即（1）中，杨勇等学者提出的嵌入确定性搜索的连续域蚁群优化算法；（3）中，Dréo J等学者提出的基于密集非递阶的连续交互式蚁群优化算法CIACA。

1.嵌入确定性搜索的连续域蚁群优化算法

嵌入确定性搜索的连续域蚁群优化算法在全局搜索过程中，利用信息素强度和启发式函数确定蚂蚁的移动方向；而在局部搜索过程中，嵌入了确定性搜索，以改善寻优性能，加快收敛速率。

设优化函数为max Z=f（X），m只蚂蚁随机分布在定义域内，每只蚂蚁都有一个邻域，其半径为r。每只蚂蚁在自己的领域内进行搜索，当所有蚂蚁完成局部搜索后，蚂蚁个体根据信息素强度和启发式函数在全局范围内进行移动，完成一次循环后，则进行信息素强度的更新计算。

（1）局部搜索

局部搜索是指每只蚂蚁在自己的邻域空间内进行随机搜索。设新的位置点为X＇，如果新的位置值比原来目标函数值大，则取新位置，否则舍去。局部搜索是在半径为r的区域内进行的，且r随迭代次数的增加而减少。有

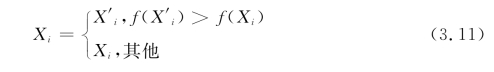
（2）全局搜索

全局搜索是指每只蚂蚁都经过一次局部搜索后，选择停留在原地，转移到其他蚂蚁的邻域或进行全局随机搜索。设Act（i）为第i只蚂蚁选择的动作，favg为m只蚂蚁的目标函数平均值，则有

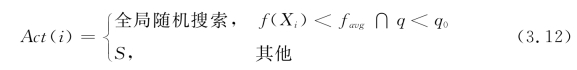
其中，q为一个在区间［0，1］内的随机数；q0是一个算法参数（0≤q0≤1）；S按以下转移规则选择动作

其中，dij=f（Xi）-f（Xj），且当i≠j时，dij＜0；而当i=j时，dij=0。式（3.13）保证了第i只蚂蚁按概率向其他目标函数值更大的蚂蚁j的邻域移动，其中系数T的大小决定了这个概率函数的斜率。

蚂蚁向某个信息素强度高的地方移动时，可能会在转移路途中的一个随机地点发现新的食物源，这里将其定义为有向随机转移。第i只蚂蚁向第j只蚂蚁的邻域转移的公式为

其中，0＜ρ＜1；ρ0＞0；a＜1。

（3）信息素强度更新规则

全局搜索结束后，要对信息素强度进行更新。更新规则为：如果有n只蚂蚁向蚂蚁j处移动（包括有向随机搜索），则有

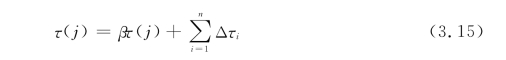
其中，是遗忘因子。

以上3个步骤模仿了自然界蚂蚁寻食的过程，蚂蚁个体通过局部随机搜索寻找食物源，然后利用信息素交换信息，决定全局转移方向。全局随机搜索的蚂蚁承担搜索陌生新食物源的任务，本质上也是一种随机性搜索算法。

（4）嵌入确定性搜索

随机性搜索算法存在着求解效率较低、求解结果较分散等缺点，因此有必要引入确定性搜索，对其加以改进。这里考虑使用确定性搜索中的直接法，直接法只利用函数信息而不需要利用导数信息，甚至不要求函数连续，适用面较广，易于编程，避免复杂计算。常用的直接法包括网格法、模式搜索法、二坐标轮换法等，本书中采用了模式搜索法中的步长加速法。

步长加速法是在坐标轮换法的基础上发展起采的，包括探测性搜索和模式性移动两部分。首先依次沿坐标方向探索，称之为探测性搜索；然后经此探测后求得目标函数的变化规律，从而确定搜索方向并沿此方向移动，称之为模式移动。重复以上两步，直到探测步长小于充分小的正数ε为止。

嵌入确定性搜索的蚁群优化算法，是在局部搜索时以一定的概率利用步长加速法进行确定性搜索。局部搜索规则如下

其中，v是随机数且0＜vv0v0＜1。

嵌入确定性搜索的蚁群优化算法的具体步骤如下：

初始化；

Loop；

每只蚂蚁处于每次循环的开始位置；

Loop；

每只蚂蚁利用式（3.16）进行局部搜索；

Until所有蚂蚁完成局部搜索；

Loop；

每只蚂蚁进行全局搜索，按式（3.13）～式（3.15）选择要进行的动作；

Until所有蚂蚁完成全局搜索；

按式（3.15）进行信息素强度更新；(www.xing528.com)

Until中止条件。

2.基于密集非递阶的连续交互式蚁群优化算法（CIACA）

基于密集非递阶的连续交互式蚁群优化算法（Continuous Interacting Ant Colony Algorithm，CIACA）的思想源于对自然界中真实蚁群行为和求解连续域优化问题蚁群优化算法机理的进一步研究。该算法通过修改蚂蚁信息素的留存方式和蚂蚁的行走规则，并运用信息素交流和直接通信两种方式来指导蚂蚁寻优。CIACA是一种崭新的蚁群优化算法。在介绍CIACA之前，先了解一下密集非递阶的生物学概念。

1）密集非递阶的概念和简单的非递阶算法

（1）密集非递阶的概念

“密集非递阶（Dense Heterarchy）”最早由Wilson E D于1988年提出。“蚁群是一个特殊的层次结构，可称之为非递阶结构。这意味着较高层次单元的性质在一定程度上影响着较低的一层，而被较高层次影响后的较低层次单元会反过来影响较高层次”，这一思想提出了两种通信通道，即基于信息素轨迹交流通信通道和蚂蚁个体间直接通信通道，这两种通信通道对于蚁群优化算法非常重要。“密集非递阶”用于描述蚁群从环境中接受“信息流”方式的一个基本概念，每只蚂蚁都可以在任意时刻与其他蚂蚁进行联络，而蚁群中的信息流是通过多个通信通道传输的。

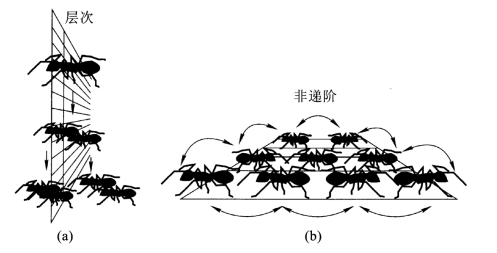
图3.4　层次结构与非递阶结构示意图

为了形象说明密集非递阶结构与层次结构的不同，参考图3.4。层次结构是一种金字塔形的结构，就像是部队中军长传令给师长，师长传令给旅长，其余以此类推。而密集非递阶结构中，“蚁后”并不传令给其他蚂蚁，而是作为蚁群网络中的普通一员，这种没有“层次”的系统具有很强的自组织功能。

（2）简单的非递阶算法

这里先介绍一个简单的非递阶算法，该算法利用了通信通道的基本思想，一个通信通道是信息素的存放地，可以用来传递多种信息，如图3.5所示。

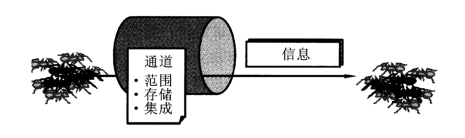
图3.5　信息通道示意图

信息通道的基本性质如下。

①范围：即蚁群中信息素的交流方式，蚁群中的某一子群可以与另一子群进行信息交流。

②存储：即信息素在系统中的驻留方式，信息素可以在某一时间段内被一直保留。

③集成：即信息素在系统中的进化方式，信息素可以通过一个外部过程被一只或多只蚂蚁更新，也可以不更新。

上述性质都集聚于同一信息通道，这样就形成了许多不同种类的信息通道。蚂蚁通信中所传递的信息具有多种形式，有时很难描述某些特殊类别的信息。

2）CIACA通信通道

按照采用通信通道的不同，定义了三种版本的CIACA。即信息素交流的CIACA，利用个体之间的直接通信的CIACA和二者协同的CIACA。

（1）信息素交流的CIACA

第一个版本的CIACA与Bilchev G A等学者率先提出的用于求解连续域优化问题的改进蚁群优化算法很接近。该算法受蚂蚁的信息素存留启发而设置了一个通信通道，每只蚂蚁在其搜索空间内的某一节点上释放一定量的信息素，节点上的信息量与其所搜索到的目标函数值成正比。这些信息节点能够被蚁群中的所有个体察觉，并逐渐消失。蚂蚁根据路径距离和路径上的信息量来决定是否选择这些信息节点。蚂蚁会向着信息素点集云的重心Gj移动，而重心位置依赖于第i个节点上第j只蚂蚁的“兴趣”ωij，表示如下

其中，n表示节点数目；xi表示第i个节点的位置；¯δ表示蚁群中两只蚂蚁间的平均距离；θi表示第i个节点上的信息量；δij表示从第j只蚂蚁到第i个节点之间的距离。

值得注意的是，处于信息素节点上的蚂蚁并不径直地向信息素点集云的重心移动。事实上，每只蚂蚁都有在蚁群中均匀分布的参数调整范围，每只蚂蚁都得到一个允许范围内的随机距离，蚂蚁会以随机距离为度量向着其重心位置移动，但是某些干扰因素可能会影响蚂蚁所到达的最终位置。

从非递阶概念的角度来描述上述行为，该CIACA中信息素交流通道的性质如下。

①范围：当蚁群中某只蚂蚁留下一定量的信息素后，其他后继蚂蚁都能觉察到该信息素的存在。

②存储：某一时间段内信息素将被一直保留于蚁群系统之中。

③集成：由于信息素的挥发作用，随着时间的推移信息素将被更新。

（2）利用个体之间的直接通信的CIACA

每只蚂蚁都能给另一只蚂蚁发送“消息”，这意味着该通信通道的范围是“点对点”式的。蚂蚁可以将已经接收到或将要接收到的信息存储到栈中，而栈中的信息可以被随机读取。此处所发送的“消息”是信息发送者的位置，即目标函数值。信息接收者会将发送者所发送来的“消息”与其自身的信息相比较，以决定它是否要向信息发送者的位置移动。最终位置将出现在一个以信息发送者为中心、信息接收者范围为半径的超球体内，然后信息接收者将“消息”进行压缩并将其随机发送给另一只蚂蚁。此时，该CIACA中的信息通道具有以下性质。

①范围：当蚁群中的某只蚂蚁发出“消息”后，仅有一只蚂蚁可以觉察到此“消息”。

②存储：某一时间段内信息可以以“记忆”的形式保存在蚁群系统中。

③集成：所存储的信息是静态的。

（3）二者协同的CIACA

信息素交流的CIACA和利用个体之间的直接通信的CIACA具有很大的不同，自组织的作用可以将较低层次的个体整合成较高层次的整体。基于这一思想，可以将上述两种版本的CIACA算法中的简单通信通道融合于一个系统中，由于通信通道没有并发机制，所以实现起来很容易。

3）CIACA

CIACA的程序结构流程如图3.6所示，算法步骤主要包括以下3步。

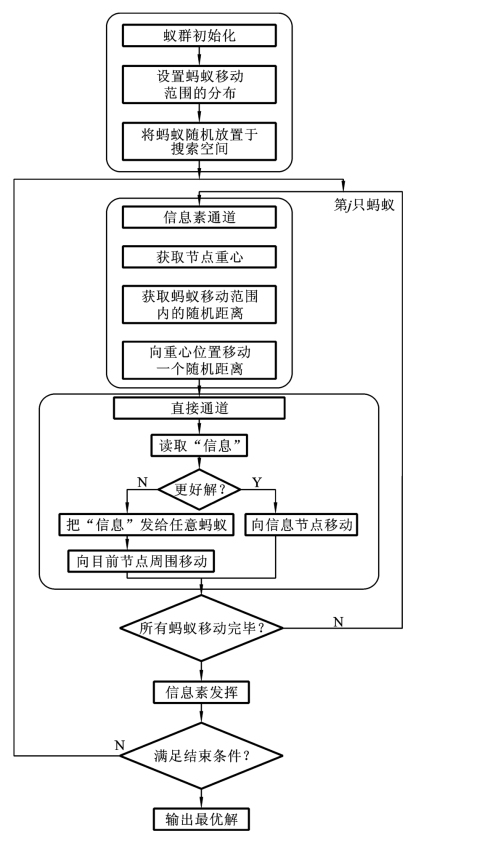
图3.6　CIACA的程序结构流程框图

第1步：设置参数。

第2步：算法开始。

第3步：若满足结束条件，算法结束。

蚂蚁根据其在通信通道系统中所处理的感知信息进行移动，需要设置4个参数。

①η∈［0，+∞）：系统中蚂蚁的数目，其值可以通过式（3.19）获得

其中，d表示目标函数的维数；ηmax表示最大蚂蚁数目，一般设置ηmax=1000；η0表示目标函数维数为0时的蚂蚁数目，一般设置η0=5；p表示蚂蚁数目的相对重要性，一般设置p=l0。

②σ∈［0，1］：搜索空间度的百分比，用来定义蚂蚁移动范围分布的标准偏差，其经验值为0.9。

③ρ∈［0，1］：用来定义信息素的持久性，其经验值为0.1。

④μ∈［0，+∞）：“消息”的初始数目，其值可以通过公式获得。