离散域蚁群优化算法的改进

国内外关于离散域蚁群优化算法的改进研究成果很多，如自适应蚁群优化算法、基于信息素扩散的蚁群优化算法、基于去交叉局部优化策略的蚁群优化算法、多态蚁群优化算法、基于模式学习的小窗口蚁群优化算法、基于混合行为蚁群优化算法、带聚类处理的蚁群优化算法、基于云模型理论的蚁群优化算法、具有感觉和知觉特征的蚁群优化算法、具有随机扰动特性的蚁群优化算法、基于信息熵的改进蚁群优化算法，等等。这里不能一一列举，仅介绍离散域优化问题的自适应蚁群优化算法。

什么是自适应蚁群优化算法？即对蚁群优化算法的状态转移概率、信息素挥发因子、信息量等因素采用自适应调节策略为一种基本改进思路的蚁群优化算法。下面介绍自适应蚁群优化算法中两个最经典的方法，一个是蚁群系统（Ant Colony System，ACS），另一个是最大—最小蚁群系统（MAX—MIN Ant System，MMAS）。

1.蚁群系统（Ant Colony System，ACS）

蚁群系统（Ant Colony System，ACS）模型最早是由Dorigo，Gambardella等学者在基本蚁群优化算法（AS）的基础上提出的。下面介绍ACS蚁群系统模型的构成和算法。

ACS解决了基本蚁群优化算法在构造解过程中，随机选择策略造成的算法进化速度慢的缺点。该算法在每一次循环中仅让最短路径上的信息量作更新，且以较大的概率让信息量最大的路径被选中，充分利用学习机制，强化最优信息的反馈。ACS的核心思想是：蚂蚁在寻找最佳路径的过程中只能使用局部信息，即采用局部信息对路径上的信息量进行调整；在所有进行寻优的蚂蚁结束路径的搜索后，路径上的信息量会再一次调整，这次采用的是全局信息，而且只对过程中发现的最好路径上的信息量进行加强。ACS模型与AS模型的主要区别有3点：①蚂蚁的状态转移规则不同；②全局更新规则不同；③新增了对各条路径信息量调整的局部更新规则。下面展开介绍。

（1）ACS的状态转移规则

为了避免停滞现象的出现，ACS采用了确定性选择和随机性选择相结合的选择策略，并在搜索过程中动态调整状态，转移概率。即对位于城市i的蚂蚁k按照式（3.5）选择下一个城市

其中，Jk（i）是第k只蚂蚁在访问到城市i后尚需访问的城市集合，q为一个在区间［0，1］内的随机数，q0是一个算法参数（0≤q0≤1）；当q＞q0时，蚂蚁k根据式（3.1）确定由城市i向下转移的目标城市。

式（3.5）所确定的蚂蚁转移到下一个城市的方法称为自适应伪随机概率选择规则（Pseudo-Random Proportional Rule）。在这种规则下，每当蚂蚁要选择向哪一个城市转移时，就产生一个在［0，1］范围内的随机数，根据这个随机数的大小按公式（3.5）确定用哪种方法产生蚂蚁转移的方向。

（2）ACS全局更新规则

在ACS蚁群优化算法中，全局更新不再用于所有的蚂蚁，而是只对每一次循环中最优的蚂蚁使用。更新规则如下式：

且

其中，Lgb为蚁群当前循环中所求得的最优路径长度；ρ为一个（0，1）区间的参数，其意义相当于蚁群优化算法基本模型中路径上的信息素挥发系数。

（3）ACS局部更新规则

局部更新规则是在所有的蚂蚁完成一次转移后执行

其中，ρ为一个（0，1）区间的参数，其意义也相当于蚁群优化算法基本模型中路径上的信息素挥发系数。Δτij的取值方法有下列三种方案

①Δτij=0；

②Δτij=T0，T0为路径上信息量的初始值；

③，其中的Jk（j）表示第k只蚂蚁在访问到城市j后尚需访问的城市集合。

上述采用Δτij取值的第③种方案的ACS算法被称为Ant-Q强化学习的蚁群优化算法。实验结果表明与AS基本蚁群优化算法相比较，Ant-Q system模型具有一般性，而且更有利于全局搜索。

算法的实现过程可以用以下的伪代码来表示

begin

初始化过程：　

ncycle=1；　

bestcycle=1；　

Δτij（i，j）=τ0=C；α；β；ρ；q0；　

ηij（由某种式算法确定）；　

tabuk=∅；　while（not termination condition）　

｛for（k=1；k＜m；k++）　　

｛将m个蚂蚁随机放置于初始城市上；｝　for（index=0；inedx＜n；index++）（index为当前循环中已经走过的城市个数）　

｛for（k=0；k＜m；k++）　　

｛产生随机数q｝　　

按式（3.5）和式（3.1）规则确定每只蚂蚁将要转移的位置；　　

将刚刚选择的城市j加入到tabuk中；　　

按式（3.8）执行局部更新规则；　　　

｝(www.xing528.com)

确定本次循环中找到的最佳路径L=min（Lk），k=1，2，…，m；

根据式（3.6）和式（3.7）执行全局更新规划；　　

ncycle=ncycle+1；

输出最佳路径及结果：

end.

2.最大—最小蚂蚁系统（MAX—MIN Ant System，MMAS）

通过对蚁群系统的研究表明，将蚂蚁搜索行为集中到最优解的附近可以提高解的质量和收敛速度，从而改进算法的性能。但是这种搜索方式会使算法过早收敛而出现早熟现象。针对这个问题，德国学者StützleT和Hoos H H提出了最大—最小蚂蚁系统（MAX—MIN ant system，MMAS）。

MMAS的基本思想：仅对每一代中的最好个体所走路径上的信息量作调整，从而更好地利用了历史信息，以加快收敛速度。但这样更容易出现过早收敛的停滞现象，为了避免算法过早收敛于非全局最优解，将各条路径上的信息量限制在区间［Tmin，Tmax］之内，超出这个范围的值将被限制为信息量允许值的上、下限，这样可以有效地避免某条路径上的信息量远大于其他路径而造成的所有蚂蚁都集中到同一条路径上，从而使算法不再扩散，加快收敛速度。MMAS是解决TSP、QAP等离散域优化问题的最好蚁群优化算法之一，许多对蚁群优化算法的改进算法都渗透着MMAS的思想。

MMAS蚁群优化算法在基本蚁群优化算法（AS）的基础上作了三点改进：

（1）首先初始化信息量Tij（t）=c设为最大值Tmax。

（2）其次各个蚂蚁在一次循环后，只有找到最短路径的蚂蚁才能够在其经过的路径上释放信息素。即

（3）最后将τij（t）限定在［τmin，τmax］之间，如果τij（t）＜τmin，则τij（t）=τmin；如果τij（t）＞τmax，则τij（t）＞τmax。

算法的实现过程可以用以下的伪代码来表示

begin

初始化过程：

ncycle=1；

bestcycle=1；

τmax；τmin；τij=τmax；Δτij=0；

ηij（由某种启发式算法确定）；

tabuk=∅

while（not termination condition）　　

｛将m个蚂蚁随机放置于初始城市上；｝　

for（index=0；inedx＜n；index++）（index为当前循环中已经走过的城市个数）　

　以概率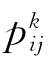（t）选择下一个城市j，j∈allowe dk（t）；　　

将刚刚选择的城市j加入到tab uk中；　　

按公式（3.8）执行局部更新规则；　　

ncycle=ncycle+1；

确定本次循环中找到的最佳路径L=min（Lk），k=1，2，…，m；

根据式（3.9）、式（3.10）计算｝（ncycle），τij（ncycle+1）；

如果τij（t）＜τmin，τij（t）=τmin；

如果τij（t）＞τmaxτij（t）=τmax；

输出最佳路径及结果：

end。

除了以上两种自适应改进蚁群优化算法外，还有许多离散域改进蚁群优化算法。虽然这些改进策略的侧重点和改进形式不同，但其目的是相同的，即避免陷入局优，缩短搜索时间，提高蚁群优化算法的全局收敛性能。