智能优化算法理论与应用-收敛性分析成果

蚁群优化算法的发展需要坚实的理论基础，这方面的工作还极其缺乏。关于蚁群优化算法收敛性的数学证明并不太多，大多数文献只研究了某些特定的蚁群优化算法的收敛性，对于一般性蚁群优化算法的收敛性证明未给出。Gutjahr在其论文中借助图论工具证明了蚁群优化算法的收敛性，该文将问题实例转化为构造图，将可行解编码转化为构造图中的路，在此基础上，在某些给定条件下，蚁群优化算法可以任意接近1的概率收敛到全局最优解，但这只是一个初步工作。Thomas Stuezle从极限理论对一种特殊的蚁群优化算法收敛性进行了分析。孙焘等学者提出了一种可用于函数优化的简单蚂蚁算法，并对其收敛性作了研究。段海滨等学者提出与Thomas Stuezle很类似的方法，对算法的全局收敛性进行了研究。由于蚂蚁算法在实际应用中形式千变万化，蚁群优化算法最初出发点是在一个图中找最短路，本章从一个最简单的最短路问题的蚁群优化算法入手，对其收敛性及相关参数问题进行一些初步分析。

假设A、B之间有m条路径AC1B，AC2B，…，ACmB（如图3.3所示），路径长度分别为d1，d2，…，dm，不失一般性，假设d1≤d2≤…≤dm。n只蚂蚁在A、B之间往返爬行，依照蚁群优化算法，随着时间的推移，大多数蚂蚁应在路径AC1B上，那么就认为A、B之间的最短路径是AC1B，下面推导寻找最短路的蚁群优化算法的选择AC1B的概率接近1的条件。

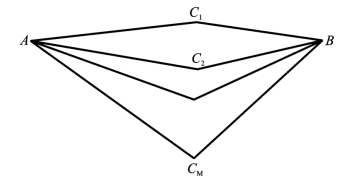
图3.3　最短路问题

假设qi，k表示蚂蚁爬行第k趟后留在路径ACiB上的平均信息素，pi，k表示蚂蚁爬行第k趟后选择路径ACiB上的平均概率。初始时刻，各条路径上的信息量相等，均为C。

定理3.1　当α≥0，β≥0时，q1，k≥q2，k≥…≥qm，k，p1，k≥p2，k≥…≥pm，k，k=1，2，…。

证　当α≥0，β≥0时，则

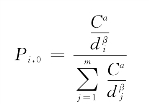
由d1≤d2≤…≤dm，可知p1，0≥p2，0≥pm，0

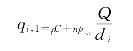
从而q1，0≥q2，0≥…≥qm，0

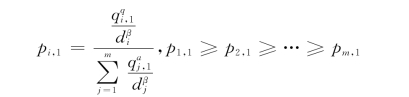
以此类推，得到

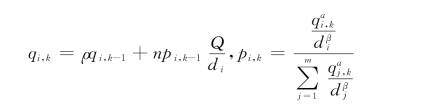
由数学归纳法可知：当α≥0，β≥0时，q1，k≥q2，k≥…≥qm，k，p1，k≥p2，k≥…≥pm，k。

定理3.1　说明每趟运行完后，AC1B上的平均信息素最多，选择路径AC1B上平均概率最大。

定理3.2　当a≥1，β≥0时，k=1，2，…，m，j=2，3，…，m。

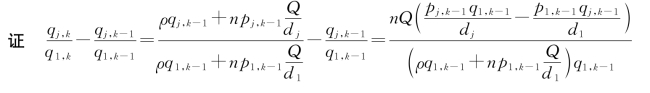(www.xing528.com)

若要，即要求：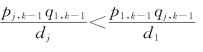

把pj，k-1和p1，k-1的公式代入上式得到：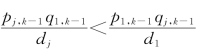

化简得到：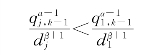

由于qj，k-1＜q1，k-1，dj＞d1，因此α≥1，β≥0就可保证。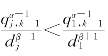

从而，k=1，2，…，m，j=2，3，…，m。

定理3.2　说明随着时间的推移越来越小。

定理3.3　当α≥1，β≥0时，p1，k＞p1，k-1，k=1，2，…m。

证　因为

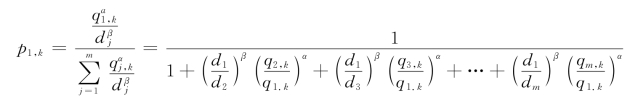
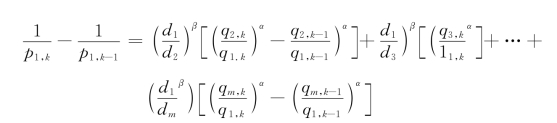
由定理3.2可知：

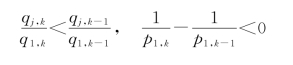
即p1，k＞p1，k-1。

定理3.3　说明随着时间的推移，选择路径AC1B的平均概率越来越大。

定理3.4　α≥1，β≥0时。

证　由定理3.3可知，α≥1，β≥0时，p1，k＞p1，k-1，序列p1，k单调递增，根据高等数学极限理论“单调递增有上界数列必有极限，且收敛到其上确界”可知，当k→∞时，。

定理3.4中的α≥1，β≥0是的充分条件，不是必要条件。定理3.4说明随着时间的推移，选择路径AC1B的平均概率接近于1。