智能优化算法模拟实验结果与分析

1.不同遗传操作组合的算法

为了考察不同遗传操作在求解TSP中的重要性，进行多种遗传操作组合的模拟实验。为了以下叙述方便，一些操作的名称采用以下方式简记：单点交叉映射法（mapping approach of single-point crossover，MSPX），单点顺序交叉法（order crossover approach of a single point，OSPX），位置信息法（position information，PIX），对换变异（reciprocal exchange mutation，REM），插入变异（insertion mutation，IM）。移位变异（translocation mutation，TM），目标导向变异（objectoriented mutation，OOM），并约定用PMX-l表示PMX中要求匹配区域无相同码，PMX-2表示对匹配区域内的码无限制，A+B表示进化过程中随机使用操作算子A和算子B，A‖B表示进化初期使用算子A，后期使用算子B。各种遗传操作组合成的算法如表2.1所示。

表2.1　各种遗传操作组合

以上各操作组合中，采用初始群体随机生成和2.3.2小节提到的选择方式一，将GA8初始群体生成改为随机产生及贪心法相结合的方式，记该算法为GA13；将GA8中的选择方式改为2.3.2小节提到的选择方式二，记该算法为GAl4。

2.模拟实验结果

对于上述各算法，分别进行了模拟实验。计算中采用的有关数据如下：群体规模100，交叉概率为0.95，变异概率为0.003，逆转判断长度l取为l/3串长，群体更新3000代结束。计算结果如表2.2所示，表中所列出的TSP路径长度为相对长度，其值由下式给出：

其中，f是由式（2.26）给出的适应度函数，式（2.26）中的常数α取为76.5。表中的时间t=clock（）/18.2，其中，clock（）为程序中调用的库函数。数字模拟实验是在奔腾IV1.4GHz处理器256MB内存的PC上实现的。表2.2中的所有数据都是经过10次测试得出的统计平均结果。

表2.2　各种遗传操作组合求解TSP问题

3.对实验结果的分析

（1）大体上来说，GA0与GAl，GA2，GA4结果无很大的差异，这说明变异算子在整个优化过程所起的作用相对小一些。这主要是变异的概率很小，使变异在整个搜索过程中发生的次数甚微造成的。但也可以注意到它们中的结果的变化还是存在规律性的。

①将GA2与GAl和GA0比较，可以看到从最佳解的角度来说，GA2要好于GAl和GA0，这说明随机使用对换变异和插入变异更容易跳出局部最优解，在一定程度上降低了陷入局部最优解的概率。分析其内在原因，可能是这两种变异机理的不同，对换变异发生一次时同时改变了4个城市之间的距离，而插入变异发生一次同时改变三个城市之间的距离，随机使用这两种变异比单一的一种操作增大了寻优的能力。

②GA3从最佳解的角度看要比GA0，GAl，GA2差。分析其原因，主要是变异算子在整个计算过程中几乎没发生过作用，因为串的长度等于城市的数目，在发生变异的前提下，再对串中的每一位按0.003的概率去判断是否通过变异概率，这样一来，实际上大大地缩减了发生变异的概率，在通过交叉陷入局部最优之后，很难跳出来。只有当串的位比较大时发生变异的机会才大，一旦发生，它的破坏作用比较大，跳出局部最优的能力也相对大一点，解决的方法是在利用移位变异时，直接增大变异概率，或定义子变异概率，这个概率的大小取决于串长。

③GA4的优化结果相对要比GA0，GAl，GA2，GA3都好，这主要是因为GA4的变异算子是单向的、目标导向的，这是由操作算子本身的机理决定的。

（2）GA5的结果与GA0的结果基本上是一致的。分析其原因，这是由交叉算子本身所决定的。OX法是保持匹配区域的位置不变：将第二个交叉点后的码作为初始码，按原顺序重新排列，删除匹配区域内存在的码，将上述得到的子串从第二个交叉点开始填充。而类OX法始终是将匹配区域移到码前，在匹配区域后依次删除匹配区域中存在的码，实际上两者的差别在于保持不变的基因片段在子代串中的位置的不同，而TSF并不取决于城市在串中的序号，TSF取决于在串中的顺序，所以这两种操作本质上是一样的，因而优化的结果也几乎是一致的。

（3）GA6的结果要比GA0与GA5的结果差。分析其原因，虽然GA6的交叉操作实质上只是将GA0和GA5中随机选取的匹配区域换成了随机选取的几个城市，但GA6的破坏作用却很大，很容易把较好的基因片段破坏掉，与GA0和GA5相比较，GA6对好的基因片段的保序能力相对差一些。

（4）GA0与GA7都是两点交叉，略去变异引起的差异，可以认为GA0的结果要明显优于GA7，分析后认为二者的主要差别在于处理TSP中约束条件的方式。为了满足约束，GA0的交叉采取在匹配区域外删除重复遍历的方式，而GA2的交叉则用映射法改变匹配区域外城市位置的方式。考虑实际上的一个较优路径，如果保持其顺序，删去若干城市，那么所得到的路径在很大程度上仍然可能保持较优。但如果把其中若干城市硬性用其他城市去代替，那么一个较优路径则很容易被破坏掉。所以针对TSP，好的基因片段保序或适应度高的串上基因的大体顺序的保持是比较重要的。

（5）GA7，GA8，GA10的结果所选用的交叉方式都采用映射改变的方法来满足约束条件。因为这种方法对原来父本中的基因片段有某种程度上的破坏作用，所以其结果相对也要差一些。

①先看GA7与GA8，二者算法类似，差别仅在于GA7要求两串的匹配区域内无相同代码。在GA7中虽然交叉点也是随机选取的，但若匹配区域很长，必然容易出现相同代码，此时只能重新选取匹配区域，所以GA7的匹配区域，即要保序的片段往往比GA8的短。在匹配区域以外的破坏要比GA8的相对小一些。需要指出的是，以下所说的保序能力的高低对应于保序片段的大小，对串的破坏性是指对匹配区域以外的部分而言的。通常认为，一个好的交叉操作应满足在进化的初期，对串的破坏性要相对大一些，保序的片段要相对小一些，以促进适应度高的个体的产生；在进化的晚期，对串的破坏性要小一些，保序的片段要相对大一些，以对适应度高的个体给予适当的保护。这样看来，GA7与GA8的差别一方面在于匹配区域本身，另一方面是由匹配区域内确定的映射在匹配区域外所引起的破坏性问题上。这样GA7与GA8相对比较，在进化的不同时期也有其不同的优点。这是造成结果无规律的一个原因。

②从GA8与GAl0的结果分析也验证了上面的分析。GA8与GAl0的区别，仅在于一个是两点交叉，一个是单点交叉。由于在TSP中，有效路径的长度只与城市的排列次序有关，而与出发点的城市位置无关，所以，对GA8的任一个交叉过程，可以设想为在交叉前增加一个操作，使得在保证对应城市次序不变的前提下，适当改变初始城市的位置，将匹配区域移至最后，这样，两点交叉实际上变成了单点交叉。可见，二者在方法上是一致的。其差别也归结到匹配区域的长度和由匹配区域内确定的映射在匹配区域外所引起的破坏性问题上。它们的结果也无大异，但无规律可循。为了进一步验证我们的分析，增加了算法GA9。下面分析GA9。

（6）GA9同GA8的差别是在初期使用PMX法，后期使用OX法。GA9的结果明显优于GA8，在一定程度上也优于GA5。前面已经说明了PMX法的保序性比OX法弱，其破坏性比OX法大。这样在迭代的初始阶段，可以用PMX法来模拟自然界的最初进化过程，扩大算法的搜索空间，产生更多的子代品种，在迭代到获得较好的局部解时，采用OX法，利用OX法得到的子代就可以较多地保留父代的基因片段。

（7）GA0与GA11的差别仅在于一个是两点交叉，一个是单点交叉。可以从这样的角度去看GA11，它是一个特殊的两点交叉，其第二个交叉点不能随机选取，而是被固定在最后一个位置，因此，GA0与GA11在方法上是一致的。二者的差别在于匹配区域统计平均长度不同。GA0的匹配区域长度期望值是1/3串长，而GA11的匹配区域长度期望值是l/2串长。就GA11来说，它相对于GA0的基因保序能力高，破坏性小。一方面好的基因片段容易存活下来，不受破坏；另一方面差的基因相对难以进化。所以，它和GA0在进化的不同阶段也有各自的优点。

（8）GAl2的优化质量、优化效率明显要比其他算法差。这是由于在GA12中没有保留匹配区域，使得子代与亲代间的遗传信息在迭代过程中大量丧失。由此可见，一般来说，匹配区域长度的适当设定，即基因片段的保序是必需的。这一点在GA6中已经得到了验证。

（9）比较GAl3与GA8的优化结果表明，对初始群体的产生施以一定的优化，对优化结果的影响可能并不大，但可以提高优化效率。

（10）比较GA14与GA8的结果可以看出，GAl4的结果略优于GA8，分析表明适应度函数的适当选取对优化的效果是重要的。如何选取适应度，要考虑到适应度函数是否在整个遗传操作过程中都适合于用来评价解的状态，而且是否利于体现“优胜劣汰”的原则。适当的适应度函数不仅可以提高优化结果，而且可以提高优化效率。

最后，针对上述讨论中多次提到的匹配区域的长度与对匹配区域外的破坏性的关系上作一点讨论。这里以交叉操作时采取映射变换删去匹配区域外重复码为例进行讨论。当匹配区域较长时，该区域直接传递给子代，故保持父本信息的程度也较高；匹配区域较短时，重复遍历较少，故此时破坏作用较小，较多地保留了父代信息；匹配区域适中时，子代匹配区域保留父代信息并不充分，匹配区域外被破坏掉的基因反而较多，故此时保留父本信息的程度最低。所以，匹配区域长度如何选取，与基因个数的多少是否有何具体关系，也仍是一个值得探讨的问题。

总体上说，算法GA4和GA11在解的质量和寻优的速度上优于其他算法。从相对长度的总和与花费时间的总和上看，算法GA11和GA12分别是最优和最差的算法。图2.6～图2.9为n=200，400，600，800时分别由算法GA4，GA11，GA11，GA11得到的最佳路线图。(www.xing528.com)

图2.6　n=200时最佳路线图

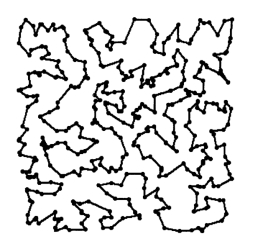
图2.7　n=400时最佳路线图

图2.8　n=600时最佳路线图

图2.9　n=800时最佳路线图

4.选择方式对优化结果的影响

为了考察选择方式对TSP优化结果的影响，下面在GA0中将选择方式改为联赛选择方法，记该算法为GA0*。将所得的结果列于表2.3，表2.3中所有数据都是经过10次测试得出的统计平均结果。由于算法GA0和GA0*在运行相同代数的时间基本一致，所以表2.3中没有列出算法的执行时间。

表2.3　选择操作优化结果影响的比较（600个城市）

从表2.3中可以看到进化早期GA0*比GA0具有更快的收敛速度，但最终结果却要差于GA0。分析如下：

由于初始群体随机产生，则初始群体中存在最优个体的概率为其中，w为解空间的大小，m为解空间中最优个体的数目，N为取定的群体规模。考虑交叉算子和变异算子的作用，在第t次迭代中生成的新个体的数目为n=N（pc+pm）prpt，其中，pc为交叉概率，pm为变异概率，pr为第t次迭代生成的个体彼此不重复的概率，pt为第t次迭代生成的个体与历代群体中个体不重复的概率，则第t次迭代过程中能够生成最优个体的概率为

其中，λt为由于选择算子的作用，后一次遗传迭代比前一次更容易生成最优个体的比率。项N（pc+pm）prpt不仅和设定的参数有关系，而且和选择、交叉算子本身的作用机制有着复杂的关系.对于算法GA0和GA0*该项是相同的，能否尽快生成最优个体取决于“入”即选择方式。联赛选择方式比按比例选择方式具有更大的λt，但它不能保证上一代群体中的个体都有机会被选择到下一代，算法的收敛性得不到保证，而GA0的选择方式保证了算法的收敛性，所以，虽然GA0*具有较快的收敛速度，但很容易陷入局部最优解，最终得不到很好的结果。

5.进化逆转对优化结果的影响

在求解TSP时引入进化逆转操作的作用是使给定的串改良到它的局部极点。为了考察进化逆转操作的局部搜索能力，下面在GA0中将逆转判断长度由l/3串长扩大到整个串长。这样，一个串中任意两位码均有机会进行逆转判断，记该算法为GA0＇。对于n=800测试得到的优化路径统计结果为108.42，明显优于GA0的111.03，但它的运行时间却长达127.72（s），相当于GA0的运行时间59.09（s）的两倍。可见进化逆转操作有它自身的两重性：一方面，它的局部搜索能力强，相对于同样的群体更新步数，若扩大逆转判断长度，则容易搜索到较好的局部极点；另一方面，进化逆转操作执行起来耗时较多。考虑到上述原因，在执行GA0＇时将群体更新步数减少至1400次，所得的结果列于表2.4中，表2.4中相应于GA0的测试结果仍为执行群体更新步数3000次时所得。

表2.4　进化逆转操作对优化结果影响的比较

分析上述实验结果可见，GA0＇在路径优化结果与运行时间上总体要比GA0好。为了进一步考察进化逆转操作对于加速优化收敛的作用，在所列出的算法实验结果最差的一个算法GA12中，改变其逆转判断长度，将它由1/3串长调至整个串长，记此时算法为GA12＇。在执行GA12＇时将群体更新步数减少至1400次，所得的结果仍列于表2.4中。表2.4中相应于GA12的测试结果仍为执行群体更新步数3000次时所得。可以看到GAl2，在路径优化结果与运行时间上总体要比GAl2好。这说明进化逆转对加速优化收敛是有效的。通过对群体更新步数的减少，可以在很大程度上削减该操作对整体运行时间的影响。考虑到该操作运行需要较长的时间，可以针对不同城市数目，适当选择逆转判断长度，以使得优化质量、优化效率达到最佳。

在测试过程中，我们发现每次测试的路径最优解之间波动较大，而运行时间波动较小。经分析认为，进化逆转操作此时已经充分发挥了作用，但某些可行解可能陷入局部最优。为了克服这种倾向，增大了变异概率，使其由原来的0.003增至0.3，记此时算法为GA12″。仍设定群体更新1400步，对于n=600，再次重复上述实验，将各次测试获得的最优路径、方差与GA12＇的相应结果进行了比较，如表2.5所示。

表2.5　进化逆转操作对优化路径结果影响的比较

表2.5中平均误差按式（2.34）计算

其中，xi为每次测试获得的数值，n为测试次数。由表2.5可见，GA12″已使运算结果得到进一步改善，表明了增加变异概率对算法的性能的影响。在对于GA12＇和GA12″分别进行的10次测试中，GA12″的方差已仅为GA12＇的21%。