智能优化算法：免疫遗传算法

本节介绍一种基于免疫的改进遗传算法，该算法是生命科学中免疫原理与传统遗传算法的结合。算法的核心在于免疫算子的构造，而免疫算子又是通过接种疫苗和免疫选择两个步骤来完成的。同时，在理论上免疫算法是概率l收敛的。

遗传算法是一类基于“产生+测试”方式的迭代搜索算法，尽管算法在一定条件下具有全局收敛特性，但算法的交叉、变异、选择等操作一般都是在概率意义下随机进行的，虽保证了种群的群体进化性，但一定程度上不可避免退化现象的出现。此外，尽管遗传算法具有通用性的一面，但却忽视了问题特征信息的辅助作用，同时相对固定的遗传操作使得对不同问题的求解缺少灵活性。大量相关研究表明，仅仅依赖于以遗传算法为代表的进化算法在模拟人类智能化处理事物能力方面还远远不足，还需要更深入地挖掘和利用人类的智能资源，而免疫遗传算法就是将生命科学中免疫的原理与遗传算法相结合来提高算法的整体性能，并有选择、有目的地利用待求解问题中的一些特征信息来抑制优化过程中退化现象的出现。

1.免疫遗传算法

类似于生物自然科学的免疫理论，免疫算子分为全免疫（full immunity）和目标免疫（target immunity），两者分别对应于生命科学中非特异性免疫和特异性免疫。其中，全免疫是指种群中每个个体在遗传算子作用后，对其每一环节进行一次免疫操作；目标免疫则是指在进行了遗传操作后，经过一定的判断，个体仅在作用点处发生免疫反应。前者主要应用于个体进化的初始阶段，而在进化过程中基本上不发生，否则将很有可能产生“同化”现象；后者一般将伴随进化的全过程，它是免疫的一个基本算子。

实际的操作过程中，首先对所求解的问题（即抗原，antigen）进行具体分析，从中提取最基本的特征信息（即疫苗，vaccine）；其次，对特征信息进行处理，将其转化为求解问题的一种方案（由此方案得到的所有解的集合称为基于上述疫苗所产生的抗体，antibody）；最后，将此方案以适当的形式转化为免疫算子，以实施具体操作。需要说明的是，待求解问题的特征信息往往不止一个，也就是说针对某一特定抗原所能提取的疫苗也可能不止一个，那么在接种疫苗过程中可以随机地选取一种疫苗进行注射，也可以将多个疫苗按照一定的逻辑关系进行组合后再注射。总而言之，免疫的思想主要是在合理提取疫苗的基础上，通过接种疫苗和免疫选择两个操作来完成的。前者以提高适应度，后者以防止种群的退化。

（1）接种疫苗

对于个体x，对其接种疫苗是指按照先验知识来修改其某些基因位上的基因，使所得个体以较大的概率具有更高的适应度。

实现考虑以下两种特殊情况：

其一，若个体y的每一基因位上的信息都是错误的，即每一位码都与最佳个体不同，则对任一个体x，x转移到y的概率为0.

其二，若个体x的每一基因位都是正确的，即x已是最佳个体，则x以概率1转移为x。

假设种群c=（x1，x2，…，xn0），对种群c接种疫苗是指在c中按比例a（0＜a≤1）随机抽取na=an个个体而进行的操作。疫苗是从对问题的先验知识中提炼出来的，它所包含的信息量及其正确性对算法的性能起着重要的作用。

（2）免疫选择

该操作分两步完成。第一步是免疫检测，即对接种了疫苗的个体进行检测，若其适应度仍不如父代，说明在交叉、变异的过程中出现了严重的退化现象。此时该个体将被父代中所对应的个体所取代；如果子代适应度优于父代则进行第二步处理。第二步是退火选择，即在当前子代种群Ek=（x1，x2，…，xn0）中以概率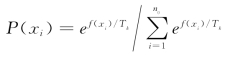选择个体xi进入新的父代种群，其中f（xi）为xi的适应度，｛Tk｝为趋于0的温度序列。

至此，给出免疫遗传算法如下，其流程如图2.2所示。

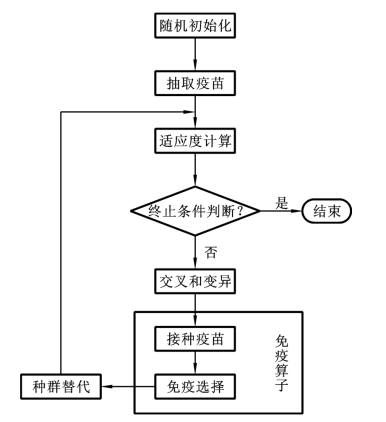
图2.2　免疫遗传算法流程框图

Step1　随机产生初始父代种群A1。

Step2　根据先验知识抽取疫苗。

Step3　若当前种群中包含了最佳个体，则结束算法；否则进行以下步骤。

Step4　对当前第k代父代种群A，进行交叉操作，得到种群Bk。

Step5　对种群Bk进行变异操作，达到种群CA。

Step6　对种群Ck进行接种疫苗操作，得到种群Dk。

Step7　对种群Dk进行免疫选择操作，得到新一代父代种群Ak+1，返回Step3。

2.免疫遗传算法的收敛性

设种群的规模为n0且在算法中保持不变，种群中所有个体均为l位的q进制编码，算法中的交叉操作选择一点或多点均可，变异操作是对每个基因位以概率PM相互独立地进行变异。算法的状态转移情况可以用随机过程来表示，其中Ak到Dk的状态转移构成一个马氏链。设X为个体搜索空间，种群可以视为状态空间S=中的一个点，|S|为S的规模，si∈S为一个种群表示随机变量V在第k代处于状态si，记（xi）｝为最优状态集。(www.xing528.com)

定义2.2　若对任意初始分布，均则称算法收敛。

该定义表明：所谓算法收敛，即指当算法迭代到足够多的次数以后，群体中包含全局最佳个体的概率接近于1，亦即算法以概率l收敛。

定理2.7　免疫遗传算法是概率1收敛的，若算法中略去免疫算子，则该算法将不再保证收敛到全局最优值，或者说该算法是强不收敛的。

3.免疫算子的机理

免疫算子是由接种疫苗和免疫选择两部分操作构成的。其中，疫苗是指依据人们对待求问题所具备的先验知识而从中提取出的一种基本的特征信息，抗体是指根据这种特征信息而得出的一类解。前者可以看做是对待求的最佳个体所能匹配模式（schema）的一种估计，后者则是对这种模式进行匹配而形成的样本。从对算法的描述中不难发现，疫苗的正确选择对算法的运行效率具有十分重要的意义。疫苗如同遗传算法的编码一样，是免疫操作得以有效地发挥作用的基础与保障。但需说明的是，选取疫苗的优劣，生成抗体的好坏，只会严重影响到免疫算子中接种疫苗作用的发挥，不至于涉及到算法的收敛性。因为免疫遗传算法的收敛性，归根结底是由免疫算子中的免疫选择来保证的。

下面考察免疫选择在算法运行过程所起到的作用。

定理2.8　在免疫选择作用下，若疫苗使抗体适应度得到提高，且高于当前群体的平均适应度，则疫苗所对应的模式将在群体中呈指数级扩散；否则，它将被遏制或呈指数级衰减。

可见，免疫选择在加强接种疫苗方面具有积极作用，在消除其负面影响方面具有鲁棒性。考虑到免疫遗传算法的应用对象主要是NP类问题，而这类问题在规模较小时一般易于求解，或者说易于发现其局部条件下的求解规律。因此，在选取疫苗时，既可以根据问题的特征信息来制作免疫疫苗，也可以在具体分析的基础上考虑降低原问题的规模，增设一些局部条件来简化问题，用简化后的问题求解规律来作为选取疫苗的一种途径。但是，在实际的选取过程中应考虑到：一方面，原问题局域化处理越彻底，则局部条件下的求解规律就越明显，这时虽然易于获取疫苗，但寻找所有这种疫苗的计算量会显著增加；另一方面，每个疫苗都是利用某一局部信息来探求全局最优解，即估计该解在某一分量上的模式，所以没有必要对每个疫苗做到精确无误。因此一般可以根据对原问题局域化处理的具体情况，选用目前通用的一些迭代优化算法来提取疫苗。

4.免疫算子的执行算法

为表述方便，令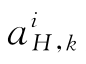为对第k代第i个个体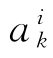接种疫苗后所得到的抗体，PI为个体接种疫苗的概率，PV为更新疫苗的概率，V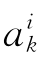，hj）表示按模式hj，修改个体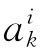上基因的接种疫苗操作，n和m分别为群体和疫苗的规模。那么，在针对某一待求问题而构造和应用免疫算子时所进行的过程如下所示：

1）抽取疫苗：

（1）分析待求问题，搜集特征信息；

（2）依据特征信息估计特定基因位上的模式H=｛hj；j=1，2，…，m｝。

2）令k=0，j=0。

3）While（Conditions=True）：

（1）若｛PV｝=True，则j=j+1；

（2）i=0；

（3）for（i≤n）：

①接种疫苗：

②免疫检验：若，则；否则；

③=i+1；

④退火选择：Ak+1=S（Ak），k=k+1。

其中，停机条件可以采用最大迭代次数或统计个体最佳适应度连续不变的最大次数。