智能优化算法的收敛性分析

1.预备知识

定义2.1　称n×n方阵A=（aij）为

（1）非负的，记A≥0，若aij≥0，i，j=1，2，…，n。

（2）严格正的，记A＞0，若aij＞0，i，j=1，2，…，n。

（3）正则的，若A≥0，且存在自然数k，使Ak＞0。

（4）随机的，若A≥0，，i=1，2，…，n。

（5）归纳的，若A≥0且经过相同的行和列初等交换后可转化为的形式为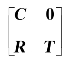的形式，其中C和T均为方阵。

（6）不可约的，若A≥0且不归约。

（7）稳定的，若A是随机的且所有行相同。

（8）列容的，若A是随机的且每一列中至少有一个正数。

引理2.1　若C，M和S为随机阵，且M＞0，S为列容的，则CMS＞0。

证明　记A=CM，B=AS。由于C为随机阵，则C的每一行中至少存在一个正数。从而，∀i，j∈｛1，2，…，n｝，即A＞0。进而，由于S为列容的，∀i，j∈｛1，2，…，n｝，故CMS＞0得证。

引理2.2　若P为正则随机阵，则Pk收敛到一个全正稳定随机阵，即P∞=［1，1，…，1］T［p1，p2，…，pm］，其中［p1，p2，…，pm］P=［p1，p2，…，pm］，，即［p1，p2，…，pm］T是PT的特征值是1且各分量均为正数的特征向量。

引理2.3　若

是随机的，其中C为m维严格正随机方阵，R≠0，T≠0，则

是一个稳定的随机阵，其中

同时，

其中，pi＞0（1≤j≤m），pj=0（m+1≤j≤n）。

2.基本遗传算法的马氏链描述

在SGA中，令所有个体形成的有限空间为Ω，所有种群对应的整个状态空间为G，其中每一种群为一个状态，一旦染色体长度l和种群数目N给定且有限时，则Ω的维数|Ω|有限，G的维数|G|=|Ω|N也有限。由于算法中每一代状态的转移依赖于选择（复制）、交叉和变异操作，且与进化代数无关，因此SGA可以视为一个有限状态的齐次马氏链。

鉴于算法中三个遗传操作是循环往复执行的，我们按“交叉→变异→选择”顺序来考虑算法中状态的转移。从而，表征马氏链的状态转移矩阵P为矩阵C，M和S的乘积，其中C，M和S分别为交叉、变异和选择操作所决定的状态转移矩阵。

（1）交叉操作

交叉操作可以视为状态空间上的随机函数，记交叉操作决定的状态转移矩阵为C=（cij）|G|×|G|，其中cij为从状态i经交叉操作转移到状态j的概率。由于一个状态通过交叉操作总要转移到状态空间中的另一个状态，因显然成立，即C为随机矩阵。

（2）变异操作

在SGA中，变异操作是独立作用于种群内各个体的每一位基因上，记变异操作决定的状态转移矩阵为M=（mij）|G|×|G|，其中mij为从状态i经交叉操作转移到状态j的概率。由于染色体的每个基因具有相同的变异概率pm＞0，则，其中Hij为状态i与状态j之间具有不同基因的位置的总数。例如状态｛（1000），（0111），（1010）｝与状态｛（1100），（1100），（0101）｝之间的Hij为7。因此，M为严格正的随机矩阵。

（3）选择操作

在SGA中，交叉和变异操作后得到的种群经选择操作后又将转移到另一个种群，记选择操作决定的状态转移矩阵为S=（sij）|G|×|G|。考虑比例选择（轮盘赌）策略，种群中染色体Xi被选中的概率为

则种群i经选择操作后保持不变的概率(www.xing528.com)

因此，转移矩阵S是随机且列容的。

通过对上述三个操作的概率描述，我们对SGA的马氏链描述有了一个清晰的认识，下面将对算法的收敛性进行阐述。

3.基本遗传算法的收敛性

对应于有限状态马氏链的一般遗传算法（二进制或十进制编码）均是后文介绍的GASA混合策略的一种特例，本节仅讨论基于二进制编码的SGA的收敛性。

定理2.2　若SGA中交叉概率pc∈［0，1］，变异概率pm∈（0，1），并且算法采用比例选择策略，则SGA的状态转移矩阵P=CMS是严格正的。

证明　利用上节矩阵C，M和S的定义以及引理2.1即可。

注：根据上述定理可知，SGA是一个遍历马氏链，从而存在一个与初值无关的极限分布，由此算法的初始种群可以任意初始化，同时任何时刻从一个状态转移到另一个状态的概率不为0，即马氏链构成了强连通图。然而，尽管初始种群的随机性在理论上不影响极限分布，但由于实际算法中由于某些环节的近似处理（如终止准则），算法的搜索结果存在一定的波动性，通常算法要执行多次才能得到较可靠的结果。

定理2.3　SGA不能够以概率1收敛到全局最优解。

证明　令P（t）=｛X1（t），X2（t），…，XN（t）｝为算法第t代的种群，其最优适配值为Zt=max｛f（Xk（t）），k=1，2，…，N｝，设f*为全局最优的适配值。由定理2.2和引理2.2知，SGA以任意状态i为极限分布的概率，因此，

注：上述定理从概率意义上说明了SGA不能够收敛到全局最优，其原因在于算法中最优解的概率遗失。因此，只要在算法中每代保留当前最优解，无论是在选择之前还是在选择之后，算法将最终收敛到全局最优，从而有以下定理。

定理2.4　每代在选择操作后保留最优解的SGA以概率l收敛到全局最优解。

证明　由于算法采用了保优技术，为方便起见，我们将保留下来的各代的最优个体存放在种群的第一号位置，但它不参与遗传操作。即，在第t代进化时的种群为（X*（t-1），X1（t），X2（t），…，XN（t）），其中X*（t-1）表示算法搜索至第t-1代所得到的最佳个体。从而，算法对应马氏链的状态空间维数将变为|Ω|N+1。然后，我们将包含相同的最优解的状态仍按在原状态空间的顺序进行排列，而对包含不同最优解的状态按最优解的适配值从大到小进行排列。由此，新的交叉、变异和选择操作对应的状态转移矩阵可以表示为C+=diag（C，C，…，C），M+=diag（M，M，…，M）和S+=diag（S，S，…，S）。

在选择操作后，算法要将当前种群中的最优解与前一代保留下来最优解进行比较，这一操作也可以用矩阵U=（uij）表示。显然，状态Y（t）=（X*（t-1），X1（t），X2（t），…，XN（t））转移到Y（t+1）=（X*（t），X1（t+1），X2（t+1），…，XN（t+1））的概率为

从而，矩阵U每一行均有且只有一个元素为1，而其他元素为0。同时，考虑到状态的排列顺序，可知矩阵U为下三角矩阵。记

其中Uij为|Ω|N×|Ω|N阶矩阵，且U11为单位矩阵。从而，马氏链的一步转移矩阵为

显然，P+为可约的随机矩阵，且CMSU11严格正。进而，考虑到P+中第一位状态由好到坏的排列顺序可知

由引理2.3可知，不包含最优个体的状态在马氏链的极限分布中的概率为0，包含最优个体的状态在马氏链的极限分布中的概率和为1。从而，算法将以概率1收敛到包含全局最优个体的状态，亦即算法能够以概率l搜索到全局最优解。

定理2.5　每代在选择操作前保留最优解的SGA以概率1收敛到全局最优解。

证明过程类似于定理2.4，在此不再赘述。

除了讨论算法的收敛性，对带有保优操作的遗传算法的收敛速度进行估计也是很重要的研究内容。

设带有保优操作的遗传算法对应于有限状态维马氏链｛Zk｝，行向量π为给定每一状态的概率，P为一步转移矩阵，则经n次转移后，各状态的概率为πPn。若种群中全部个体相同且均为最优，则称此状态为吸收态。显然，马氏链｛Zk｝中有以下三种性质的状态：

（1）吸收态；（2）可一步转移到吸收态的非吸收态；（3）经P可一步转移到另一状态，而此状态转移到吸收态的概率为零。从而，一步转移矩阵P可以分解为其中，Ik为描述吸收态的k阶单位矩阵，R为描述能够转移到吸收态的状态的（|G|-k）×k阶矩阵，Q为描述其他状态的（|G|-k）×（|G|-k）阶矩阵。进而

其中，Mn=I+Q+Q2+…+Qn-1，‖Q‖＜1，从而

由于SGA算法的全局收敛性，最优分布z*存在，且z*=z（0）P∞，z（0）=［z1（0），z2（0），…，zk（0），zk+1（0），…，。以下给出z（i）=z（0）Pi收敛到z*的速度估计。

定理2.6　设‖Q‖=λ＜1，则概率分布z（i）收敛到z*的收敛速度估计为‖z（i）-z*‖≤O（λi）。

证明　

迄今为止，遗传算法的理论研究仍主要针对SGA模型。高级的遗传算法由于其本身的多样性，理论方面的研究相当分散，尚未取得引人注目的结果。同时，大部分结论都是通过计算机数值仿真来说明的，数学上严格完整且令人信服的解释仍需努力探索。GA的收敛性研究，尤其是如何提高算法的收敛速度和鲁棒性，仍是具有重要研究价值的课题。