量子PCA算法步骤及特征向量估计

用一系列指数逼近的想法基于贝克坎贝尔-豪斯多夫（Baker Campbell-Hausdorff）公式，表述为

式中，Z=logeXeY，X 和Y 是非对易（non-commuting）变量。这样的结果就是李积公式（Lie product formula）

由此，为了计算汉密尔顿函数，先计算

式中，d=maxidi。这是哈密顿分量（Component Hamiltonians）的误差项，所以为了得到总误差ϵ，必须对ϵ/（nmd2）进行调整。因此，如果汉密尔顿函数是局部的，模拟系统的时间复杂度是线性的。

任意但稀疏的汉密尔顿系统，其系统组件之间的相互作用可能不是局部的。一个作用在n 个量子位上的汉密尔顿量H 是稀疏的，条件是它在每行或每列中有最多有常数个非零项。而且，H被一个常数所限制。在这种情况下，可选择一个任意的正整数k，模拟汉密尔顿函数需要O（（log∗n）t1+1/2k）次对H 的矩阵元素的访问（Berry等，2007）【98】。此处的log∗n是迭代对数：

也就是说，在结果小于或等于1之前，必须多次递归调用对数函数。虽然复杂度接近线性，但稀疏模拟的亚线性缩放（sublinear scaling）是不可行的[98]。(www.xing528.com)

为了模拟非稀疏的、任意的高维汉密尔顿函数，典型的方法是高阶Trot⁃ter-Suzuki 展开，这需要O（d log d）的时间复杂度来计算一个汉密尔顿分量【126】。通过在另一个密度矩阵σ 上使用一个密度矩阵ρ 作为汉密尔顿量，仅可以将其简化到O（log d）的时间复杂度【125】。使用对第一个变量的部分跟踪和交换操作符S，得到

量子PCA的算法步骤：

步4 用eiρt进行了量子相位估计算

步5 输出ρ的特征向量|χi>，对匹配特征值的估计̂。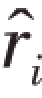

传统机器学习技术面临的挑战是处理大规模、高维度的数据。量子机器学习算法通过结合传统机器学习算法和量子模型来优化传统机器学习算法，可以有效地解决传统的经典计算机在计算量极大的情况下存在的一些问题。通过把数据映射到量子态上，可以使同类问题的空间复杂度得到指数级的下降。